
 ,设
,设 .
. ,
, 表示
表示 ;
; 的值.
的值.
 ,我们易根据向量加法的三角形法则,用
,我们易根据向量加法的三角形法则,用 ,
, 表示
表示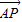 ;
; ,我们易将向量
,我们易将向量 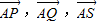 ,用
,用  ,
, 表示,利用向量加减法的运算法则,易得到
表示,利用向量加减法的运算法则,易得到  .
. ,同理C,Q,M三点共线,存在实数m,n使得
,同理C,Q,M三点共线,存在实数m,n使得 ,且m+n=1,综合即得结论.
,且m+n=1,综合即得结论. ,
, ,∴
,∴ ….(3分)
….(3分) ,∴
,∴ .
.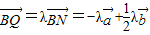 ,①
,① ,∴
,∴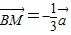 ,又
,又
 ,且m+n=1,
,且m+n=1, ,②
,② ,
, ,∴
,∴ …..(10分)
…..(10分)

 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
| MP |
| 1 |
| 3 |
| PN |
查看答案和解析>>
科目:高中数学 来源: 题型:
| MP |
| MN |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知M,N分别在△ABC的边AB和AC上,且
已知M,N分别在△ABC的边AB和AC上,且| AM |
| MB |
| AN |
| NC |
| AB |
| a |
| AC |
| b |
| a |
| b |
| AP |
| |BQ| |
| |QN| |
查看答案和解析>>
科目:高中数学 来源: 题型:
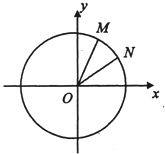 如图,在平面直角坐标系xoy中,以Ox轴为始边做两个锐角α,β,且α,β的终边依次与单位圆O相交于M、N两点,已知M、N的横坐标分别为
如图,在平面直角坐标系xoy中,以Ox轴为始边做两个锐角α,β,且α,β的终边依次与单位圆O相交于M、N两点,已知M、N的横坐标分别为2
| ||
| 5 |
3
| ||
| 10 |
| m |
| n |
| 2 |
| m |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
2
| ||
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com