
从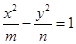 (其中
(其中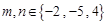 )所表示的圆锥曲线(椭圆、双曲线、抛物线)方程中任取一个,则此方程是焦点在
)所表示的圆锥曲线(椭圆、双曲线、抛物线)方程中任取一个,则此方程是焦点在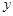 轴上的双曲线方程的概率为( )
轴上的双曲线方程的概率为( )
A.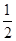 | B.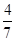 | C. | D.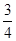 |
B
解析试题分析:由于m和n的所有可能取值共有3×3=9个,其中有两种不符合题意,故共有7种,可一一列举,从中数出能使方程是焦点在x轴上的双曲线的选法,即m和n都为正的选法数,最后由古典概型的概率计算公式即可的其概率.
设(m,n)表示m,n的取值组合,则取值的所有情况有(-1,-1),(2,-1),(2,2),(2,3),(3,-1),(3,2),(3,3)共7个,(注意(-1,2),(-1,3)不合题意)其中能使方程是焦点在x轴上的双曲线的有:(2,2),(2,3),(3,2),(3,3)共4个, ∴此方程是焦点在x轴上的双曲线方程的概率为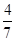 ,选B.
,选B.
考点:古典概型,双曲线的方程
点评:本题考查了古典概型概率的求法,椭圆、双曲线、抛物线的标准方程,列举法计数的技巧,准确计数是解决本题的关键。


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:单选题
下列说法正确的是
| A.互斥事件一定是对立事件,对立事件不一定是互斥事件 |
| B.互斥事件不一定是对立事件,对立事件一定是互斥事件 |
C.事件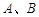 中至少有一个发生的概率一定比 中至少有一个发生的概率一定比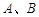 中恰有一个发生的概率大 中恰有一个发生的概率大 |
D.事件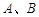 同时发生的概率一定比 同时发生的概率一定比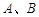 中恰有一个发生的概率小 中恰有一个发生的概率小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com