练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若0＜α＜，＜β＜0，，则

    [     ]

    A．
    B．
    C．
    D．
    D
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    e-x-2，(x≤0)
    2ax-1，(x＞0)
    （a是常数且a＞0）．对于下列命题：
    ①函数f（x）的最小值是-1；
    ②函数f（x）在R上是单调函数；
    ③若f（x）＞0在[
    1
    2
    ，+∞)    上恒成立，则a的取值范围是a＞1；
    ④对任意x1＜0，x2＜0且x1≠x2，恒有f(
    x1+x2
    2
    )＜
    f(x1)+f(x2)
    2
    ．
    其中正确命题的序号是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面直角坐标系中，角α，β的终边分别与以原点为圆心的单位圆交于A、B两点，且|
    AB
    |=
    2
    		5
    5
    ．
    （Ⅰ）求cos（α-β）的值；
    （Ⅱ）若0＜α＜
    π
    2
    ，-
    π
    2
    ＜β＜0    ，且sinβ=-
    5
    13
    ，求sinα的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设A、B是x轴上的两点，点P的横坐标为2且|PA|=|PB|．若直线PA的方程为x-y-1=0，则直线PB的方程是（　　）

    查看答案和解析>>

    科目：高中数学 来源：2010-2011年福建师大附中高一第二学期模块考试数学 题型：解答题

    设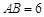，在线段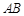上任取两点C,D（端点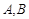除外），将线段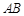分成三条线段AC,CD,DB.

    （1）若分成的三条线段的长度均为正整数，求这三条线段可以构成三角形（称事件A）的概率；

    （2）若分成的三条线段的长度均为正实数，求这三条线段可以构成三角形（称事件B）的概率；

    （3）根据以下用计算机所产生的20组随机数，试用随机数摸拟的方法，来近似计算（Ⅱ）中事件B的概率.

    20组随机数如下：

     

    1组

    2组

    3组

    4组

    5组

    6组

    7组

    8组

    9组

    10组

    X

    0.52

    0.36

    0.58

    0.73

    0.41

    0. 6

    0.05

    0.32

    0.38

    0.73

    Y

    0.76

    0.39

    0.37

    0.01

    0.04

    0.28

    0.03

    0.15

    0.14

    0.86

     

     

    11组

    12组

    13组

    14组

    15组

    16组

    17组

    18组

    19组

    20组

    X

    0.67

    0.47

    0.58

    0.21

    0.54

    0. 64

    0.36

    0.35

    0.95

    0.14

    Y

    0.41

    0.54

    0.51

    0.37

    0.31

    0.23

    0.56

    0.89

    0.17

    0.03

    （X是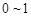之间的均匀随机数，Y也是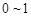之间的均匀随机数）

     

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （20）设f(x)是定义在[0, 1]上的函数，若存在x*∈(0，1)，使得f(x)在[0, x*]上单调递增，在[x*，1]上单调递减，则称f(x)为[0, 1]上的单峰函数，x*为峰点，包含峰点的区间为含峰区间．

        对任意的[0，1]上的单峰函数f(x)，下面研究缩短其含峰区间长度的方法．

    （I）证明：对任意的x1，x2∈(0，1)，x1＜x2，若f(x1)≥f(x2)，则(0，x2)为含峰区间；若f(x1)≤f(x2)，则(x1，1)为含峰区间；

    （II）对给定的r（0＜r＜0.5），证明：存在x1，x2∈(0，1)，满足x2－x1≥2r，使得由（I）所确定的含峰区间的长度不大于 0.5＋r；

    （III）选取x1，x2∈(0, 1)，x1＜x2，由（I）可确定含峰区间为(0，x2)或(x1，1)，在所得的含峰区间内选取x3，由x3与x1或x3与x2类似地可确定一个新的含峰区间．在第一次确定的含峰区间为(0，x2)的情况下，试确定x1，x2，x3的值，满足两两之差的绝对值不小于0.02，且使得新的含峰区间的长度缩短到0.34.

    （区间长度等于区间的右端点与左端点之差）

    查看答案和解析>>

    同步练习册答案