
【题目】函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,方程
时,方程![]() 在区间
在区间![]() 内有唯一实数解,求实数
内有唯一实数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2) ![]() 或
或![]()
【解析】
(1)先求得函数![]() 的导函数和定义域,对
的导函数和定义域,对![]() 分成
分成![]() 等
等![]() 种情况,分类讨论函数的单调性.(2)将
种情况,分类讨论函数的单调性.(2)将![]() 分离常数化为
分离常数化为![]() ,构造函数
,构造函数![]() ,利用导数求得
,利用导数求得![]() 的单调性和最值,由此求得
的单调性和最值,由此求得![]() 的取值范围.
的取值范围.
(1)![]() ,
,
(i)当![]() 时,
时,![]() ,令
,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
函数![]() 在
在![]() 上单调递增,
上单调递增,![]() 上单调递减;
上单调递减;
(ii)当![]() 时,令
时,令![]() ,得
,得![]() ,
,![]()
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
函数![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,![]() 上单调递减;
上单调递减;
(iii)当![]() 时,
时,![]() ,函数f(x)在
,函数f(x)在![]() 上单调递增;
上单调递增;
(iv)当![]() 时,
时,![]()
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]()
函数![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,![]() 上单调递减;
上单调递减;
综上所述:当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]()
(2)当![]() 时,
时,![]() ,由
,由![]() ,得
,得![]() ,
,
又![]() ,所以
,所以![]() ,要使方程
,要使方程![]() 在区间
在区间![]() 上有唯一实数解,
上有唯一实数解,
只需![]() 有唯一实数解,
有唯一实数解,
令![]() ,∴
,∴![]() ,
,
由![]() 得
得![]() ;
;![]() 得
得![]() ,
,
∴![]() 在区间
在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上是减函数.
上是减函数.
![]() ,
,![]() ,
,![]() ,故
,故![]() 或
或![]()


科目:高中数学 来源: 题型:
【题目】对于由2n个质数组成的集合![]() ,可将其元素两两搭配成n个乘积,得到一个n元集.若
,可将其元素两两搭配成n个乘积,得到一个n元集.若![]() 与
与![]() 是由此得到的两个n元集,其中,
是由此得到的两个n元集,其中, ![]() ,且
,且![]() ,则称集合对{A ,B}是由M炮制成的一幅“对联”(如由四元集{a,b,c,d}可炮制成三幅对联:
,则称集合对{A ,B}是由M炮制成的一幅“对联”(如由四元集{a,b,c,d}可炮制成三幅对联:
![]()
![]() .
.
求六元质数集M={a,b,c,d,e,f}所能炮制成的对联数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当
指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当![]() 数值大于或等于20.5时,我们说体重较重,当
数值大于或等于20.5时,我们说体重较重,当![]() 数值小于20.5时,我们说体重较轻,身高大于或等于
数值小于20.5时,我们说体重较轻,身高大于或等于![]() 我们说身高较高,身高小于170cm我们说身高较矮.
我们说身高较高,身高小于170cm我们说身高较矮.
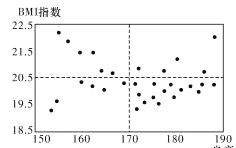
(1)已知某高中共有32名男体育特长生,其身高与![]() 指数的数据如散点图,请根据所得信息,完成下述列联表,并判断是否有
指数的数据如散点图,请根据所得信息,完成下述列联表,并判断是否有![]() 的把握认为男生的身高对
的把握认为男生的身高对![]() 指数有影响.
指数有影响.
身高较矮 | 身高较高 | 合计 | |
体重较轻 | |||
体重较重 | |||
合计 |
(2)①从上述32名男体育特长生中随机选取8名,其身高和体重的数据如表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根据最小二乘法的思想与公式求得线性回归方程为![]() .利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献值(保留两位有效数字)
.利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献值(保留两位有效数字)![]() ;
;
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
残差 | 0.1 | 0.3 | 0.9 |
|
|
②通过残差分析,对于残差的最大(绝对值)的那组数据,需要确认在样本点的采集中是否有人为的错误,已知通过重新采集发现,该组数据的体重应该为![]() .请重新根据最最小二乘法的思想与公式,求出男体育特长生的身高与体重的线性回归方程.
.请重新根据最最小二乘法的思想与公式,求出男体育特长生的身高与体重的线性回归方程.
(参考公式)
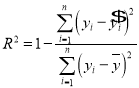 ,
,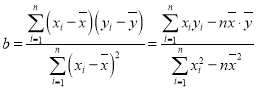 ,
,![]() ,
,![]() ,
,![]() .
.
(参考数据)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
0.10
0.05
0.01
0.005
![]()
2.706
3.811
6.635
7.879
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() :
:![]() 的焦点,抛物线
的焦点,抛物线![]() 上的点
上的点![]() 满足
满足![]() (
(![]() 为坐标原点),且
为坐标原点),且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() :
:![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,是否存在实数
,是否存在实数![]() 及定点
及定点![]() ,对任意实数
,对任意实数![]() ,都有
,都有![]() ?若存在,求出
?若存在,求出![]() 的值及点
的值及点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为维护交通秩序,防范电动自行车被盗,天津市公安局决定,开展二轮电动自行车免费登记、上牌照工作.电动自行车牌照分免费和收费(安装防盗装置)两大类,群众可以 自愿选择安装.已知甲、乙、丙三个不同类型小区的人数分别为15000,15000,20000.交管部门为了解社区居民意愿,现采用分层抽样的方法从中抽取10人进行电话访谈.
(Ⅰ)应从甲小区和丙小区的居民中分别抽取多少人?
(Ⅱ)设从甲小区抽取的居民为![]() ,丙小区抽取的居民为
,丙小区抽取的居民为![]() .现从甲小区和丙小区已抽取的居民中随机抽取2人接受问卷调查.
.现从甲小区和丙小区已抽取的居民中随机抽取2人接受问卷调查.
(ⅰ)试用所给字母列举出所有可能的抽取结果;
(ⅱ)设![]() 为事件“抽取的2人来自不同的小区”,求事件
为事件“抽取的2人来自不同的小区”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将高二(1)班的四个同学分到语文、数学、英语三个兴趣小组,每个兴趣小组至少有一名同学的分配方法有多少种?下列结论正确的有( )
A.![]() B.
B.![]()
C.![]() D.18
D.18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com