
设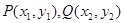 是抛物线
是抛物线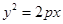
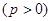 上相异两点,
上相异两点,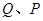 到y轴的距离的积为
到y轴的距离的积为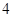 且
且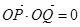 .
.
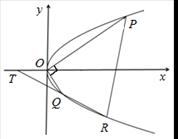
(1)求该抛物线的标准方程.
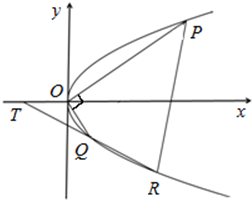
(2)过Q的直线与抛物线的另一交点为R,与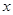 轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值.
轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值.
(1)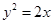 .(2)直线PQ垂直于x轴时|PR|取最小值
.(2)直线PQ垂直于x轴时|PR|取最小值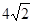 .
.
【解析】
试题分析:(1)确定抛物线的标准方程,关键是确定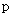 的值.利用
的值.利用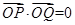 ,可得
,可得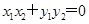 ,
,
再根据P、Q在抛物线上,得到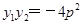 ,集合已知条件
,集合已知条件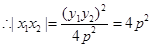 ,得4p2=4,p=1.
,得4p2=4,p=1.
(2)设直线PQ过点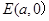 ,且方程为
,且方程为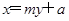 ,应用联立方程组
,应用联立方程组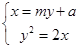
消去x得y2 2my 2a=0,利用韦达定理,建立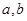 的方程组,确定
的方程组,确定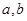 得到
得到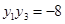 ,利用“弦长公式”求解.
,利用“弦长公式”求解.
试题解析: (1)∵ ·=0,则x1x2+y1y2=0, 1分
又P、Q在抛物线上,故y12=2px1,y22=2px2,故得
+y1y2=0, y1y2= 4p2
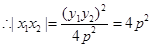 3分
3分
又|x1x2|=4,故得4p2=4,p=1.
所以抛物线的方程为: 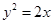 5分
5分
(2)设直线PQ过点E(a,0)且方程为x=my+a
联立方程组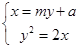
消去x得y2 2my 2a=0
∴ 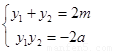 ①
7分
①
7分
设直线PR与x轴交于点M(b,0),则可设直线PR方程为x=ny+b,并设R(x3,y3),
同理可知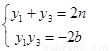 ②
9分
②
9分
由①、②可得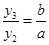
由题意,Q为线段RT的中点,∴ y3=2y2,∴b=2a
又由(Ⅰ)知, y1y2= 4,代入①,可得
2a= 4 ∴ a=2.故b=4. 11分
∴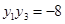
∴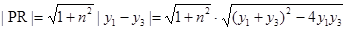
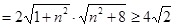 .
.
当n=0,即直线PQ垂直于x轴时|PR|取最小值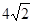 14分
14分
考点:抛物线标准方程,直线与抛物线的位置关系.


科目:高中数学 来源: 题型:
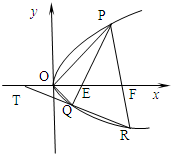 设P(x1,y1),Q(x2,y2) 是抛物线C:y2=2px(p>0)上相异两点,且
设P(x1,y1),Q(x2,y2) 是抛物线C:y2=2px(p>0)上相异两点,且| OP |
| OQ |
| TR |
| TQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•济南二模)设P(x1,y1),Q(x2,y2)是抛物线y2=2px(p>0)上相异两点,Q、P到y轴的距离的积为4且
(2013•济南二模)设P(x1,y1),Q(x2,y2)是抛物线y2=2px(p>0)上相异两点,Q、P到y轴的距离的积为4且| OP |
| OQ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,设P(x1,y1),Q(x2,y2)是抛物线C:y2=2px(p>0)上相异两点,且
如图,设P(x1,y1),Q(x2,y2)是抛物线C:y2=2px(p>0)上相异两点,且 ,直线QP与x轴相交于E.
,直线QP与x轴相交于E. ,若存在,求出F点的坐标(用p表示),若不存在,说明理由.
,若存在,求出F点的坐标(用p表示),若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:2007年广东省汕头市高考数学二模试卷(理科)(解析版) 题型:解答题
 设P(x1,y1),Q(x2,y2) 是抛物线C:y2=2px(p>0)上相异两点,且
设P(x1,y1),Q(x2,y2) 是抛物线C:y2=2px(p>0)上相异两点,且 ,直线PQ 与x 轴相交于E.
,直线PQ 与x 轴相交于E. ,若存在,求出F 点的坐标(用p 表示),若不存在,说明理由.
,若存在,求出F 点的坐标(用p 表示),若不存在,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com