Question

甲、乙两船驶向一个不能同时停泊两艘船的码头，它们在一昼夜内到达该码头的时刻是等可能的.如果甲船停泊时间为1 h，乙船停泊时间为2 h，求它们中的任意一艘都不需要等待码头空出的概率.

Answer 1

分析：这是一个几何概型问题,首先根据题意建立关于时间的不等式，然后画图通过线性规划的知识求解.

解：设甲、乙两艘船到达码头的时刻分别为x与y，A为“两船都需要等待码头空出”，则0≤x≤24，0≤y≤24，且基本事件空间为Ω={（x，y）|x∈［0，24］，y∈［0，24］}.

要使两船都不需要等待码头空出，当且仅当甲比乙早到达1 h以上或乙比甲早到达2 h以上，即y-x≥1或x-y≥2，

故A={（x，y）|y-x≥1或x-y≥2，x∈［0，24］，y∈［0，24］}.

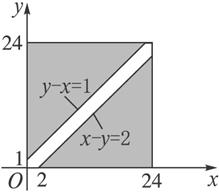
∴A为图中阴影部分，Ω为边长是24的正方形，由几何概率定义，

知所求概率为P（A）=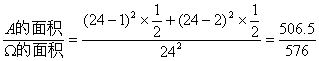

=0.87934.

绿色通道

    问题的关键是要构造出随机事件对应的几何图形，利用图形的几何度量来求随机事件的概率.