
| π |
| 2 |
|
|
|
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2cosθ |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| 4 | 2 |
| 2 |


科目:高中数学 来源:陕西省师大附中2009届高三第二次模拟考试(数学) 题型:044
(理)已知a>0,函数f(x)=![]() ,x∈(0,+∞).设0<x1<
,x∈(0,+∞).设0<x1<![]() ,记曲线y=f(x)在点M(x1,f(x1))处的切线为l
,记曲线y=f(x)在点M(x1,f(x1))处的切线为l
(1)求l的方程;
(2)设l与x轴交点为(x2,0),求证:①0<x2≤![]() ;②若0<x1<
;②若0<x1<![]() ,则x1<x2<2x1
,则x1<x2<2x1
查看答案和解析>>
科目:高中数学 来源:天津高考真题 题型:解答题
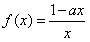 ,x∈(0,+∞),设0<x1<
,x∈(0,+∞),设0<x1<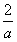 ,记曲线y=f(x)在点M(x1,f(x1))处的切线为l,
,记曲线y=f(x)在点M(x1,f(x1))处的切线为l, ;
; 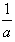 ,则x1<x2<
,则x1<x2<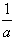 。
。 查看答案和解析>>
科目:高中数学 来源:2004-2005学年浙江省杭州市源清中学高二(上)12月月考数学试卷(理科)(解析版) 题型:解答题
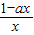 ,x∈(0,+∞).设0<x1<
,x∈(0,+∞).设0<x1<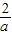 ,记曲线y=f(x)在点M(x1,f(x1))处的切线为l
,记曲线y=f(x)在点M(x1,f(x1))处的切线为l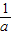 ; ②若0<x1<
; ②若0<x1<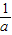 ,则x1<x2<2x1.
,则x1<x2<2x1.查看答案和解析>>
科目:高中数学 来源:2009-2010学年浙江省舟山市七校高三(下)3月联考数学试卷(理科)(解析版) 题型:解答题
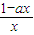 ,x∈(0,+∞).设0<x1<
,x∈(0,+∞).设0<x1< ,记曲线y=f(x)在点M(x1,f(x1))处的切线为l
,记曲线y=f(x)在点M(x1,f(x1))处的切线为l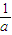 ; ②若0<x1<
; ②若0<x1<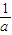 ,则x1<x2<2x1.
,则x1<x2<2x1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com