练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆：的短轴长为2，以椭圆的长轴为直径的圆与直线相切.

    （1）求椭圆的标准方程；

    （2）斜率为的直线交椭圆于，两点，且，若直线上存在点，使得是以为顶角的等腰直角三角形，求直线的方程.

    【答案】（1）；（2）

    【解析】

    （1）先由短轴长求出的值，再根据点到直线的距离公式求出的值即可；（2）设直线的方程为，先由得，则，，再根据直线上存在点，使得是以为顶角的等腰直角三角形，得出，最后由方程组即可求出的值进而求出直线的方程.

    （1）由题意得，，则，所以椭圆的方程为.

    （2）设直线的方程为，，

    由得.

    令，得，则，.

    因为是以为顶角的等腰直角三角形，

    所以平行于轴，过作的垂线，则垂足为线段的中点.

    设点的坐标为，则.

    由方程组解得，即.

    而，所以直线的方程为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝|x﹣1|，关于x的不等式f（x）＜3﹣|2x+1|的解集记为A．

    （1）求A；

    （2）已知a，b∈A，求证：f（ab）＞f（a）﹣f（b）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.

    有时可用函数

    描述学习某学科知识的掌握程度，其中x表示某学科知识的学习次数（），表示对该学科知识的掌握程度，正实数a与学科知识有关.

    （1） 证明：当时，掌握程度的增加量总是下降；

    （2） 根据经验，学科甲、乙、丙对应的a的取值区间分别为,,

    .当学习某学科知识6次时，掌握程度是85%，请确定相应的学科.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】秉承提升学生核心素养的理念，学校开设以提升学生跨文化素养为核心的多元文化融合课程.选某艺术课程的学生唱歌、跳舞至少会一项，已知会唱歌的有人，会跳舞的有人，现从中选人，设为选出的人中既会唱歌又会跳舞的人数，且

    (1)求选该艺术课程的学生人数;

    (2)写出的概率分布列并计算.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】第7届世界军人运动会于2019年10月18日至27日在湖北武汉举行，赛期10天，共设置射击、游泳、田径、篮球等27个大项，329个小项.共有来自100多个国家的近万名现役军人同台竞技.前期为迎接军运会顺利召开，武汉市很多单位和部门都开展了丰富多彩的宣传和教育活动，努力让大家更多的了解军运会的相关知识，并倡议大家做文明公民.武汉市体育局为了解广大民众对军运会知识的知晓情况，在全市开展了网上问卷调查，民众参与度极高，现从大批参与者中随机抽取200名幸运参与者，他们得分（满分100分）数据，统计结果如下：

    组别

    频数

    5

    30

    40

    50

    45

    20

    10

    （1）若此次问卷调查得分整体服从正态分布，用样本来估计总体，设，分别为这200人得分的平均值和标准差（同一组数据用该区间中点值作为代表），求，的值（，的值四舍五入取整数），并计算；

    （2）在（1）的条件下，为感谢大家参与这次活动，市体育局还对参加问卷调查的幸运市民制定如下奖励方案：得分低于的可以获得1次抽奖机会，得分不低于的可获得2次抽奖机会，在一次抽奖中，抽中价值为15元的纪念品A的概率为，抽中价值为30元的纪念品B的概率为.现有市民张先生参加了此次问卷调查并成为幸运参与者，记Y为他参加活动获得纪念品的总价值，求Y的分布列和数学期望，并估算此次纪念品所需要的总金额.

    （参考数据：；；.）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（题文）在三棱锥中，底面，，且三棱锥的每个顶点都在球的表面上，则球的表面积为 _______

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学学校对高三年级文科学生进行了一次自主学习习惯的自评满意度的调查，按系统抽样方法得到了一个自评满意度（百分制，单位：分）的样本，如图分别是该样本数据的茎叶图和频率分布直方图（都有部分缺失）．

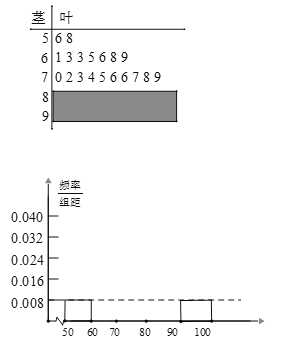
    （1）完善频率分布直方图（需写出计算过程）；

    （2）分别根据茎叶图和频率分布直方图求出样本数据的中位数m1和m2，并指出选用哪一个数据来估计总体的中位数更合理（需要叙述理由）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，分别过椭圆左、右焦点的动直线相交于点，与椭圆分别交于与不同四点，直线的斜率满足, 已知与轴重合时, .

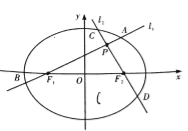
    （1）求椭圆的方程；

    （2）是否存在定点使得为定值，若存在，求出点坐标并求出此定值，若不存在，

    说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义一：对于一个函数，若存在两条距离为d的直线和，使得在时，恒成立，则称函数在D内有一个宽度为d的通道.定义二：若一个函数，对于任意给定的正数，都存在一个实数，使得函数在内有一个宽度为的通道，则称在正无穷处有永恒通道.下列函数：①；②；③.其中在正无穷处有永恒通道的函数的个数为（ ）

    A.0B.1C.2D.3

    查看答案和解析>>

    同步练习册答案