
【题目】已知a>2,求证:loga(a-1)<log(a+1)a.
【答案】【解答】
证明:∵a>2,∴a-1>1.∴loga(a-1)>0,log(a+1)a>0,
由于![]()
![]()
![]() .
.
∵a>2,∴0<loga(a2-1)<logaa2=2.
∴ ![]() ,
,
即![]() .
.
∵log(a+1)a>0,∴loga(a-1)<log(a+1)a.
【解析】本题考查作商比较法的应用,解答本题需要先判断不等式两侧代数式的符号,然后再用作商法比较左右两侧的大小.(1)当不等式的两边为对数式或指数式时,可用作商比较法来证明,另外,要比较的两个解析式均为正值,且不宜采用作差比较法时,也常用作商比较法.(2)在作商比较法中 ![]() 是不正确的,这与a、b的符号有关,比如若b>0,由
是不正确的,这与a、b的符号有关,比如若b>0,由 ![]() ,可得a>b,但若b<0,则由
,可得a>b,但若b<0,则由 ![]() 得出的反而是a<b,也就是说,在作商比较法中,要对a、b的符号作出判断,否则,结论将是错误的.对于此类问题,不外乎可分为含参数变量的和大小固定的两类,因而也可以通过特殊值的方法进行一定的猜测,进而给出一定的理性推理或证明过程.
得出的反而是a<b,也就是说,在作商比较法中,要对a、b的符号作出判断,否则,结论将是错误的.对于此类问题,不外乎可分为含参数变量的和大小固定的两类,因而也可以通过特殊值的方法进行一定的猜测,进而给出一定的理性推理或证明过程.


科目:高中数学 来源: 题型:
【题目】已知数列{bn}满足bn=| ![]() |,其中a1=2,an+1=
|,其中a1=2,an+1= ![]()
(1)求b1 , b2 , b3 , 并猜想bn的表达式(不必写出证明过程);
(2)设cn= ![]() ,数列|cn|的前项和为Sn , 求证Sn<
,数列|cn|的前项和为Sn , 求证Sn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】①设三个正实数a , b , c , 满足![]() ,求证:a , b , c一定是某一个三角形的三条边的长;
,求证:a , b , c一定是某一个三角形的三条边的长;
②设n个正实数 a1,a2,...an 满足不等式 ![]() (其中
(其中 ![]() ),求证: a1,a2,...an 中任何三个数都是某一个三角形的三条边的长.
),求证: a1,a2,...an 中任何三个数都是某一个三角形的三条边的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的各项均为正数,且a2=6,a3+a4=72.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=an﹣n(n∈N*),求数列{bn}的前n项和 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:kx﹣y+1+2k=0(k∈R).
(1)证明:直线l过定点;
(2)若直线l不经过第四象限,求k的取值范围;
(3)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线mx+ ![]() y﹣1=0在y轴上的截距是﹣1,且它的倾斜角是直线
y﹣1=0在y轴上的截距是﹣1,且它的倾斜角是直线 ![]() =0的倾斜角的2倍,则( )
=0的倾斜角的2倍,则( )
A.m=﹣ ![]() ,n=﹣2
,n=﹣2
B.m= ![]() ,n=2
,n=2
C.m= ![]() ,n=﹣2
,n=﹣2
D.m=﹣ ![]() ,n=2
,n=2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是各项为正数的等比数列,{bn}是等差数列,且a1=b1=1,b2+b3=2a3 , a5﹣3b2=7.
(1)求{an}和{bn}的通项公式;
(2)设cn=anbn , n∈N* , 求数列{cn}的前n项和为Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限x年 | 3 | 5 | 6 | 7 | 9 |
年推销金额y万元 | 2 | 3 | 3 | 4 | 5 |
(1)从编号1﹣5的五位推销员中随机取出两位,求他们年推销金额之和不少于7万元的概率;
(2)求年推销金额y关于工作年限x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;若第6名产品推销员的工作年限为11年,试估计他的年推销金额. 附:回归直线的斜率和截距的最小二乘法估计公式为:
;若第6名产品推销员的工作年限为11年,试估计他的年推销金额. 附:回归直线的斜率和截距的最小二乘法估计公式为: ![]() =
= 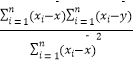 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com