
����Ŀ��ij���Թ�˾��6����Ʒ����Ա���乤������������������������±���
����Ա��� | 1 | 2 | 3 | 4 | 5 |
��������x�� | 3 | 5 | 6 | 7 | 9 |
���������y��Ԫ | 2 | 3 | 3 | 4 | 5 |
��1���ӱ��1��5����λ����Ա�����ȡ����λ�����������������֮�Ͳ�����7��Ԫ�ĸ��ʣ�
��2�������������y���ڹ�������x�����Իع鷽�� ![]() =
= ![]() x+
x+ ![]() ������6����Ʒ����Ա�Ĺ�������Ϊ11�꣬�Թ��������������� �����ع�ֱ�ߵ�б�ʺͽؾ����С���˷����ƹ�ʽΪ��
������6����Ʒ����Ա�Ĺ�������Ϊ11�꣬�Թ��������������� �����ع�ֱ�ߵ�б�ʺͽؾ����С���˷����ƹ�ʽΪ�� ![]() =
= 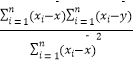 ��
�� ![]() =
= ![]() ��
�� ![]()
![]() ��
��
���𰸡�
��1���⣺�ӱ��1��5����λ����Ա�����ѡ����λ�����ǵ�����������������{2��3��1��}��{2��3��2��}��{2��4}��{2��5}��{3��1����3��2��}��{3��1����4}��{3��1����5}��{3��2����4}��{3��2����5}��{4��5}��10�֣�
������������������������7��Ԫ���������6�֣���������� ![]()
��2���⣺�ɱ������ݿ�֪�� ![]() �����Ϲ�ʽ�ɵ�
�����Ϲ�ʽ�ɵ� ![]() ��
�� ![]() ��
��
�� ![]() ��
��
�ֵ�x=11ʱ�� ![]() ��
��
�ʵ�6����Ʒ����Ա�Ĺ�������Ϊ11�꣬�������������ԼΪ5.9��Ԫ
����������1���оٻ����¼�������������ʣ���2�����������ݣ������x��y��ƽ�������ۼ���ص����ݺ������ϵ����ʽ��������ع�ϵ�����õ��������y���ڹ�������x�����Իع鷽�̣�����������Ϊ11����������������y���ڹ�������x�����Իع鷽�̣�����Ԥ�����������������Ĺ���ֵ��


 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾Ϊ�Ա���˾��160��Ա��������״�����е��飬�Ƚ�Ա��������Ϊ1��2��3������159��160������ϵͳ�����ķ������ȼ��س�ȡ��ÿ�γ�ȡһ�����壩����ȡ��һ����������֪��ȡ��Ա������С���������Ϊ5��21����ô��ȡ��Ա���У����ı��Ӧ���ǣ� ��
A.141
B.142
C.149
D.150
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪{an}�ǵȲ����У�����a10=30��a20=50��
��1��������{an}��ͨ�ʽ��
��2����bn=an��20��������{bn}��ǰn���Tn����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��
��
��1���� ![]() ������y=f��x���ĵ������䣻
������y=f��x���ĵ������䣻
��2����x=��1�Ǻ���y=f��x����һ����ֵ�㣬���жϴ�ʱ����y=f��x��������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() �Һ���y=f��x��ͼ���ϵ㣨1��f��1������������б��Ϊ0��
�Һ���y=f��x��ͼ���ϵ㣨1��f��1������������б��Ϊ0��
��1�����ú���a��ʽ�ӱ�ʾb��������f��x���ĵ����ԣ�
��2�����ں���ͼ���ϵIJ�ͬ����A��x1 �� y1����B��x2 �� y2������ں���ͼ���ϴ��ڵ�M��x0 �� y0������x0�ʣ�x1 �� x2����ʹ�õ�M��������l��AB�����AB���ڡ��������ߡ����ر�أ��� ![]() ʱ���ֳ�AB���ڡ���ֵ�������ߡ������ʣ�����f��x�����Ƿ��������A��Bʹ�������ڡ���ֵ�������ߡ��������ڣ����A��B�����꣬�������ڣ�˵�����ɣ�
ʱ���ֳ�AB���ڡ���ֵ�������ߡ������ʣ�����f��x�����Ƿ��������A��Bʹ�������ڡ���ֵ�������ߡ��������ڣ����A��B�����꣬�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x��alnx��a��R��
��1����a=2ʱ��������y=f��x���ڵ�A��1��f��1�����������߷��̣�
��2������f��x���ļ�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ȱ�����{an}�У���֪a1=2��a4=16��
��1��������{an}��ͨ�ʽan��
��2����a3 �� a5�ֱ��ǵȲ�����{bn}�ĵ�4��͵�16�������{bn}��ͨ�ʽ��ǰn���Sn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������{an}��ǰn���ΪSn �� ��{an}�� ![]() ���ǵȲ����У��ҹ�����ȣ�
���ǵȲ����У��ҹ�����ȣ�
��1��������{an}��ͨ�ʽ��
��2����bn= ![]() ��cn=bnbn+1 �� ������{cn}��ǰn���Tn ��
��cn=bnbn+1 �� ������{cn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com