
【题目】已知正项数列{an}的前n项和为Sn , 若{an}和 ![]() 都是等差数列,且公差相等.
都是等差数列,且公差相等.
(1)求数列{an}的通项公式;
(2)令bn= ![]() ,cn=bnbn+1 , 求数列{cn}的前n项和Tn .
,cn=bnbn+1 , 求数列{cn}的前n项和Tn .
科目:高中数学 来源: 题型:
【题目】某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限x年 | 3 | 5 | 6 | 7 | 9 |
年推销金额y万元 | 2 | 3 | 3 | 4 | 5 |
(1)从编号1﹣5的五位推销员中随机取出两位,求他们年推销金额之和不少于7万元的概率;
(2)求年推销金额y关于工作年限x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;若第6名产品推销员的工作年限为11年,试估计他的年推销金额. 附:回归直线的斜率和截距的最小二乘法估计公式为:
;若第6名产品推销员的工作年限为11年,试估计他的年推销金额. 附:回归直线的斜率和截距的最小二乘法估计公式为: ![]() =
= 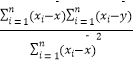 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:在数列{an}中,若an2﹣an﹣12=p,(n≥2,n∈N* , p为常数),则称{an}为“等方差数列”,下列是对“等方差数列”的有关判断:
①若{an}是“等方差数列”,则数列{ ![]() }是等差数列;
}是等差数列;
②{(﹣2)n}是“等方差数列”;
③若{an}是“等方差数列”,则数列{akn}(k∈N* , k为常数)也是“等方差数列”;
④若{an}既是“等方差数列”,又是等差数列,则该数列是常数数列.
其中正确命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC三边所在直线方程:lAB:3x﹣2y+6=0,lAC:2x+3y﹣22=0,lBC:3x+4y﹣m=0(m∈R,m≠30).
(1)判断△ABC的形状;
(2)当BC边上的高为1时,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() ,g(x)=﹣x﹣ln(﹣x)其中a≠0,
,g(x)=﹣x﹣ln(﹣x)其中a≠0,
(1)若x=1是函数f(x)的极值点,求实数a的值及g(x)的单调区间;
(2)若对任意的x1∈[1,2],x2∈[﹣3,﹣2]使得f(x1)≥g(x2)恒成立,且﹣2<a<0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是二次函数f(x)=x2﹣bx+a的部分图象,则函数g(x)=ex+f′(x)的零点所在的区间是( ) 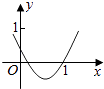
A.(﹣1,0)
B.(0,1)
C.(1,2)
D.(2,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:对于m∈[﹣1,1],不等式a2﹣5a﹣3≥ ![]() 恒成立;命题q:不等式x2+ax+2<0有解,若p∨q为真,且p∧q为假,求a的取值范围.
恒成立;命题q:不等式x2+ax+2<0有解,若p∨q为真,且p∧q为假,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cosωxsin(ωx+ ![]() )+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
)+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
(Ⅰ)求a和ω的值;
(Ⅱ)求函数f(x)在[0,π]上的单调递减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com