
【题目】已知函数f(x)=4cosωxsin(ωx+ ![]() )+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
)+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
(Ⅰ)求a和ω的值;
(Ⅱ)求函数f(x)在[0,π]上的单调递减区间.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 若{an}和 ![]() 都是等差数列,且公差相等.
都是等差数列,且公差相等.
(1)求数列{an}的通项公式;
(2)令bn= ![]() ,cn=bnbn+1 , 求数列{cn}的前n项和Tn .
,cn=bnbn+1 , 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个树形图依据下列规律不断生长:1个空心圆点到下一行仅生长出1个实心圆点,1个实心圆点到下一行生长出1个实心圆点和1个空心圆点.则第11行的实心圆点的个数是 . 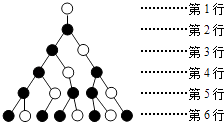
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y=3cosx的图象,只需将函数y=3sin(2x﹣ ![]() )的图象上所有点的( )
)的图象上所有点的( )
A.横坐标缩短到原来的 ![]() (纵坐标不变),所得图象再向左平移
(纵坐标不变),所得图象再向左平移 ![]() 个单位长度
个单位长度
B.横坐标缩短到原来的 ![]() (纵坐标不变),所得图象再向右平移
(纵坐标不变),所得图象再向右平移 ![]() 个单位长度
个单位长度
C.横坐标伸长到原来的2倍(纵坐标不变),所得图象再向左平移 ![]() 个单位长度
个单位长度
D.横坐标伸长到原来的2倍(纵坐标不变),所得图象再向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣x+2a﹣1(a>0).
(1)若f(x)在区间[1,2]为单调增函数,求a的取值范围;
(2)设函数f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式;
(3)设函数 ![]() ,若对任意x1 , x2∈[1,2],不等式f(x1)≥h(x2)恒成立,求实数a的取值范围.
,若对任意x1 , x2∈[1,2],不等式f(x1)≥h(x2)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率q1为0.25,在B处的命中率为q2 , 该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,其分布列为:
ξ | 0 | 2 | 3 | 4 | 5 |
p | 0.03 | 0.24 | 0.01 | 0.48 | 0.24 |
(1)求q2的值;
(2)求随机变量ξ的数学期望Eξ;
(3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项都是正数,2a5 , a4 , 4a6成等差数列,且满足 ![]() ,数列{bn}的前n项和为
,数列{bn}的前n项和为 ![]() ,n∈N* , 且b1=1
,n∈N* , 且b1=1
(1)求数列{an},{bn}的通项公式
(2)设 ![]() ,n∈N* , {Cn}前n项和为
,n∈N* , {Cn}前n项和为 ![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,记抛物线y=x﹣x2与x轴所围成的平面区域为M,该抛物线与直线y=kx(k>0)所围成的平面区域为N,向区域M内随机抛掷一点P,若点P落在区域N内的概率为 ![]() ,则k的值为( )
,则k的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com