
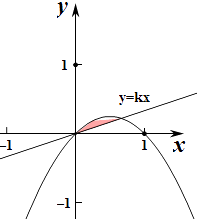
【题目】在平面直角坐标系中,记抛物线y=x﹣x2与x轴所围成的平面区域为M,该抛物线与直线y=kx(k>0)所围成的平面区域为N,向区域M内随机抛掷一点P,若点P落在区域N内的概率为 ![]() ,则k的值为( )
,则k的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:∵抛物线y=x﹣x2与x轴交于点(0,0)与(1,0),
∴根据定积分的几何意义,可得抛物线与x轴所围成的平面区域M的面积为
S=![]()
![]() (x﹣x2)dx=(
(x﹣x2)dx=( ![]() )|
)| ![]() =
= ![]() .
.
设抛物线与直线y=kx(k>0)所围成的平面区域A的面积为S',
∵向区域M内随机抛掷一点P,点P落在区域A内的概率为 ![]() ,
,
∴ ![]() =
= ![]() ,可得S'=
,可得S'= ![]() S=
S= ![]() ,
,
求出y=x﹣x2与y=kx的交点中,除原点外的点B坐标为(1﹣k,k﹣k2),
可得S'=![]()
![]() [(x﹣x2)﹣kx]dx=[
[(x﹣x2)﹣kx]dx=[ ![]() (1﹣k)x2﹣
(1﹣k)x2﹣ ![]() ]|
]| ![]() =
= ![]() (1﹣k)3.
(1﹣k)3.
因此可得 ![]() (1﹣k)3=
(1﹣k)3= ![]() ,
,
解得k= ![]() .
.
故选:A
【考点精析】认真审题,首先需要了解几何概型(几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等).


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cosωxsin(ωx+ ![]() )+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
)+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
(Ⅰ)求a和ω的值;
(Ⅱ)求函数f(x)在[0,π]上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.已知函数 ![]() .
.
(1)若f(x)是奇函数,求m的值;
(2)当m=1时,求函数f(x)在(﹣∞,0)上的值域,并判断函数f(x)在(﹣∞,0)上是否为有界函数,请说明理由;
(3)若函数f(x)在[0,1]上是以3为上界的函数,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率. 附:K2= ![]()
P(K2>k0) | 0.10 | 0.05 |
| 0.005 |
k0 | 2.706 | 3.841 |
| 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2(a﹣2)x﹣b2+13.
(1)先后两次抛掷一枚质地均匀的骰子(骰子六个面上分别标有数字1,2,3,4,5,6),骰子向上的数字一次记为a,b,求方程f(x)=0有两个不等正根的概率;
(2)如果a∈[2,6],求函数f(x)在区间[2,3]上是单调函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AA1=2AB=2BC,E,F,E1分别是棱AA1 , BB1 , A1B1的中点. 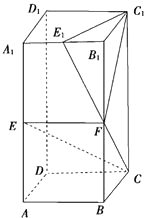
(1)求证:CE∥平面C1E1F;
(2)求证:平面C1E1F⊥平面CEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,直l线l的参数方程为 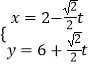 (t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=10cosθ.
(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=10cosθ.
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A、B,若点P的坐标为(2,6),求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(2x﹣m)的定义域为集合A,函数g(x)= ![]() ﹣
﹣ ![]() 的定义域为集合B.
的定义域为集合B.
(Ⅰ)若BA,求实数m的取值范围;
(Ⅱ)若A∩B=,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,雾霾日趋严重,我们的工作、生活受到了严重的影响,如何改善空气质量已成为当今的热点问题.某空气净化器制造厂,决定投入生产某型号的空气净化器,根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产该型号空气净化器x(百台),其总成本为P(x)(万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本).销售收入Q(x)(万元)满足Q(x)= ![]() ,假定该产品产销平衡(即生产的产品都能卖掉),根据以述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据以述统计规律,请完成下列问题:
(1)求利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)工厂生产多少百台产品时,可使利润最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com