直线l:y=mx+1,双曲线C:3x2-y2=1,问是否存在m的值,使l与C相交于A,B两点,且以AB为直径的圆过原点.
解:假设存在m值满足条件,
设A、B坐标分别为(x
1,y
1)(x
2,y
2),
由

得:(3-m
2)x
2-2mx-2=0,
则3-m
2≠0,且△=4m
2-4(3-m
2)(-2)>0,得m
2<6且m
2≠3①,
由韦达定理有:
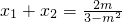
,

,
因为以AB为直径的圆过原点,所以OA⊥OB,即

,即x
1x
2+y
1y
2=0,
所以x
1x
2+(mx
1+1)(mx
2+1)=0,即(1+m
2)x
1x
2+m(x
1+x
2)+1=0,
所以(1+m
2)

+m

+1=0,解得m=±1,
故存在m=1或m=-1使l与C相交于A,B两点,且以AB为直径的圆过原点.
分析:假设存在m值满足条件,设A、B坐标分别为(x
1,y
1)(x
2,y
2),联立直线方程与双曲线方程,消掉y后得x的二次方程,有△>0,由以AB为直径的圆过原点得OA⊥OB,即

,从而可转化为关于A、B坐标的关系式,由直线方程可进一步化为x
1,x
2的式子,将韦达定理代入即可得m的方程,解出m后检验是否满足△>0即可.
点评:本题考查直线与圆锥曲线的位置关系、圆的性质,考查转化思想,解决本题的关键是正确理解“以AB为直径的圆过原点”并能合理转化.

 得:(3-m2)x2-2mx-2=0,
得:(3-m2)x2-2mx-2=0,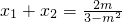 ,
, ,
, ,即x1x2+y1y2=0,
,即x1x2+y1y2=0, +m
+m +1=0,解得m=±1,
+1=0,解得m=±1, ,从而可转化为关于A、B坐标的关系式,由直线方程可进一步化为x1,x2的式子,将韦达定理代入即可得m的方程,解出m后检验是否满足△>0即可.
,从而可转化为关于A、B坐标的关系式,由直线方程可进一步化为x1,x2的式子,将韦达定理代入即可得m的方程,解出m后检验是否满足△>0即可.
