
 、
、 ,你觉得应先回答哪个问题?说明理由.
,你觉得应先回答哪个问题?说明理由. 每课必练系列答案
每课必练系列答案科目:高中数学 来源:不详 题型:解答题
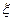 表示所得的分数,求
表示所得的分数,求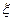 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 次;在
次;在 处每投进一球得
处每投进一球得 分,在
分,在 处每投进一球得
处每投进一球得 分;如果前两次得分之和超过
分;如果前两次得分之和超过 分即停止投篮,否则投第三次.同学在
分即停止投篮,否则投第三次.同学在 处的命
处的命 中率
中率 为
为 0,在
0,在
 处的命中率为
处的命中率为 ,该同学选择先在
,该同学选择先在 处投一球,以后都在
处投一球,以后都在 处投,用
处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为   |  |  |  |  |  |
 |  |  |  |  |  |
 的值;
的值;
 机变量
机变量 的数学期望
的数学期望 ;
; 
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的分布列及期望
的分布列及期望 ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com