
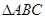 中,
中,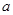 ,
,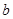 ,
,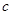 分别是角A,B,C的
分别是角A,B,C的 对边,且
对边,且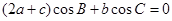 .
.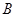 的值;
的值;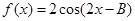 ,将
,将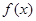 的图像向左平移
的图像向左平移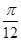 个单位长度后得到函数
个单位长度后得到函数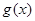 的图像,求
的图像,求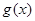 的单调增区间.
的单调增区间. B+C=π,所以 sin(B+C)=sinA,得 2sinAcosB+sinA=0,
B+C=π,所以 sin(B+C)=sinA,得 2sinAcosB+sinA=0,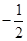 , ……………… 5分
, ……………… 5分 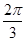 . ……………… 6分
. ……………… 6分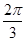 , ∴ f(x)=2cos(2x-
, ∴ f(x)=2cos(2x-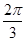 ), ………………7分
), ………………7分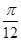 )-
)-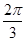 ]=2cos(2x-
]=2cos(2x-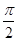 )=2sin2
)=2sin2 x, ………………9分
x, ………………9分 由2k
由2k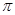 -
-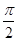 ≤2x≤2k
≤2x≤2k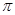 +
+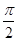 (k∈Z),得k
(k∈Z),得k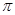 -
-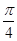 ≤x≤k
≤x≤k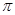 +
+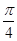 (k∈Z),
(k∈Z),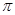 -
-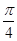 ,k
,k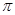 +
+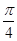 ](k∈Z)
](k∈Z)

科目:高中数学 来源:不详 题型:解答题
 =(4cos
=(4cos , sin
, sin ),
),  =(sin
=(sin , 4cos
, 4cos ),
), =(cos
=(cos , -4sin
, -4sin )(
)(
 且
且 、
、 均不等于
均不等于 ).
). 的最大值;
的最大值; ∥
∥ 且
且  ⊥(
⊥( -2
-2 )时,求tan
)时,求tan + tan
+ tan 的值.
的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com