
| x | 4 | 2 | 3 | 5 |
| y | 38 | 20 | 31 | 51 |
| A. | 60 | B. | 70 | C. | 73 | D. | 69 |
分析 根据表中数据计算$\overline{x}$、$\overline{y}$,由回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$过样本中心点,求出$\widehat{b}$的值,再计算x=7时$\widehat{y}$的值即可.
解答 解:根据表中数据,得:$\overline{x}$=$\frac{1}{4}$×(4+2+3+5)=3.5,
$\overline{y}$=$\frac{1}{4}$×(38+20+31+51)=35;
且回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$过样本中心点($\overline{x}$,$\overline{y}$),其中$\widehat{a}$=0,
所以$\widehat{b}$×3.5+0=35,解得$\widehat{b}$=10,
所以回归方程为$\widehat{y}$=10x;
当x=7时,$\widehat{y}$=10×7=70,
即广告费用为7万元时销售额为70万元.
故选:B.
点评 本题考查了线性回归方程的应用问题,是基础题目


科目:高中数学 来源: 题型:选择题

| A. | ①② | B. | ①④ | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
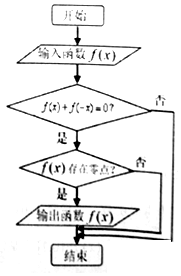 程序框图如图所示,现输入如下四个函数:f(x)=$\frac{1}{x}$,f(x)=x4,f(x)=2x,f(x)=x-$\frac{1}{x}$,则可以输出的函数是( )
程序框图如图所示,现输入如下四个函数:f(x)=$\frac{1}{x}$,f(x)=x4,f(x)=2x,f(x)=x-$\frac{1}{x}$,则可以输出的函数是( )| A. | f(x)=$\frac{1}{x}$ | B. | f(x)=x4 | C. | f(x)=2x | D. | f(x)=x-$\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{3}$ | B. | 2 | C. | $\frac{\sqrt{15}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com