
若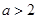 ,则函数
,则函数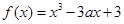 在区间
在区间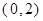 上零点的个数为
上零点的个数为
| A.0个 |
| B.1个 |
| C.2个 |
| D.3个 |
B
解析考点:函数的零点.
分析:根据a>2,分析导函数的符号,确定函数的单调性,验证f(0),f(2)的符号,结合图象可知函数f(x)=x3-3ax+3 在(0,2)上的零点个数.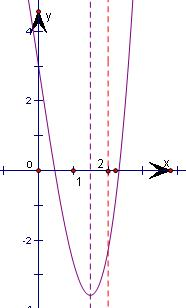
解:∵函数f(x)=x3-3ax+3
∴f′(x)=3x2-3a=3(x2-a)=3(x+ )(x-
)(x- ),
),
∵a>2,
令f′(x)>0得x> ,得函数f(x)在(
,得函数f(x)在( ,+∞)上是增函数,
,+∞)上是增函数,
令f′(x)<0可得0<x< ,得函数f(x)在(0,
,得函数f(x)在(0, )上是减函数,
)上是减函数,
而f(0)=3>0,f( )=(
)=( )3-3a
)3-3a +3=3-2a
+3=3-2a <0,
<0,
∴函数f(x)=x3-3ax+3在(0, )上零点有一个.
)上零点有一个.
又f(2)=23-3a×2+3=11-6a<0,
∴函数f(x)=x3-3ax+3在( ,2)上没有零点.
,2)上没有零点.
则函数f(x)=x3-3ax+3在区间(0,2)上零点的个数为1,
故选B.


科目:高中数学 来源: 题型:
| x2 |
| 5 |
| y2 |
| m |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
如右图(1)所示,定义在区间![]() 上的函数
上的函数![]() ,如果满
,如果满
足:对![]() ,
,![]() 常数A,都有
常数A,都有![]() 成立,则称函数
成立,则称函数
![]() 在区间
在区间![]() 上有下界,其中
上有下界,其中![]() 称为函数的下界. (提示:图(1)、(2)中的常数
称为函数的下界. (提示:图(1)、(2)中的常数![]() 、
、![]() 可以是正数,也可以是负数或零)
可以是正数,也可以是负数或零)
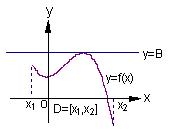 (Ⅰ)试判断函数
(Ⅰ)试判断函数![]() 在
在![]() 上是否有下界?并说明理由;
上是否有下界?并说明理由;
(Ⅱ)又如具有右图(2)特征的函数称为在区间![]() 上有上界.
上有上界.
请你类比函数有下界的定义,给出函数![]() 在区间
在区间![]() 上
上
有上界的定义,并判断(Ⅰ)中的函数在![]() 上是否
上是否
有上界?并说明理由;
(Ⅲ)若函数![]() 在区间
在区间![]() 上既有上界又有下界,则称函数
上既有上界又有下界,则称函数
![]() 在区间
在区间![]() 上有界,函数
上有界,函数![]() 叫做有界函数.试探究函数
叫做有界函数.试探究函数![]() (
(![]()
![]()
![]() 是常数)是否是
是常数)是否是![]() (
(![]()
![]() 、
、![]() 是常数)上的有界函数?
是常数)上的有界函数?
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试预测卷(广东卷)理科试题 题型:解答题
(本小题满分14分)对于定义在区间D上的函数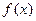 ,若存在闭区间
,若存在闭区间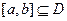 和常数
和常数 ,使得对任意
,使得对任意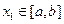 ,都有
,都有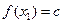 ,且对任意
,且对任意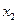 ∈D,当
∈D,当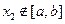 时,
时,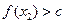 恒成立,则称函数
恒成立,则称函数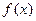 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.
(Ⅰ)判断函数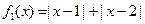 和
和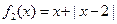 是否为R上的“平底
是否为R上的“平底 型”函数? 并说明理由;
型”函数? 并说明理由;
(Ⅱ)设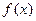 是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式
是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式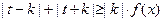 对一切
对一切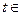 R恒成立,求实数
R恒成立,求实数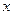 的取值范围;
的取值范围;
(Ⅲ)若函数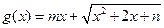 是区间
是区间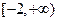 上的“平底型”函数,求
上的“平底型”函数,求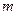 和
和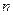 的值.
的值.
.
查看答案和解析>>
科目:高中数学 来源:广东省09-10学年高二下学期期末考试理科数学试题 题型:解答题
(本小题满分14分)对于定义在区间D上的函数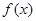 ,若存在闭区间
,若存在闭区间 和常数
和常数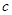 ,使得对任意
,使得对任意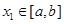 ,都有
,都有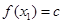 ,且对任意
,且对任意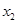 ∈D,当
∈D,当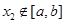 时,
时,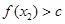 恒成立,则称函数
恒成立,则称函数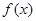 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.
(Ⅰ)判断函数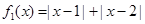 和
和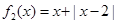 是否为R上的“平底型”函数?并说明理由;
是否为R上的“平底型”函数?并说明理由;
(Ⅱ)设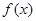 是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式
是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式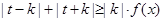 对一切
对一切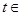 R恒成立,求实数
R恒成立,求实数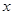 的取值范围;
的取值范围;
(Ⅲ)若函数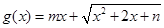 是区间
是区间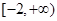 上的“平底型”函数,求
上的“平底型”函数,求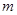 和
和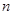 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省厦门市高三上学期末理科数学卷 题型:选择题
设函数 的定义域为D,若存在非零实数h使得对于任意
的定义域为D,若存在非零实数h使得对于任意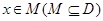 ,有
,有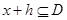 ,且
,且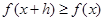 ,则称
,则称 为M上的“h阶高调函数”。给出如下结论:
为M上的“h阶高调函数”。给出如下结论:
①若函数 在R上单调递增,则存在非零实数h使
在R上单调递增,则存在非零实数h使 为R上的“h阶高调函数”;
为R上的“h阶高调函数”;
②若函数 为R上的“h阶高调函数”,则
为R上的“h阶高调函数”,则 在R上单调递增;
在R上单调递增;
③若函数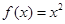 为区间
为区间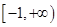 上的“h阶高诬蔑财函数”,则
上的“h阶高诬蔑财函数”,则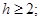
④若函数 在R上的奇函数,且
在R上的奇函数,且 时,
时,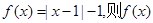 只能是R上的“4阶高调函数”。
只能是R上的“4阶高调函数”。
其中正确结论的序号为 ( )
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com