
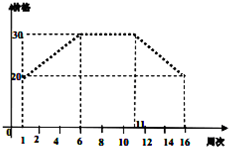
 在某服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元/件(第一周价格),并且每周价格上涨,如图所示,从第6周开始到第11轴保持30元/件的价格平稳销售;从第12周开始,当季节即将过去时,每周下跌,直到第16周周末,该服装不再销售.
在某服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元/件(第一周价格),并且每周价格上涨,如图所示,从第6周开始到第11轴保持30元/件的价格平稳销售;从第12周开始,当季节即将过去时,每周下跌,直到第16周周末,该服装不再销售.
|
|
|
|
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |


科目:高中数学 来源: 题型:
| x2 |
| 4 |
A、(-
| ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
D、(-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
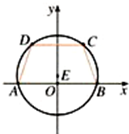 如图,等腰梯形ABCD的底边AB和CD长分别为6和2
如图,等腰梯形ABCD的底边AB和CD长分别为6和2| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x-3 |
| x-7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com