
【题目】设椭圆中心在坐标原点,A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.
(Ⅰ)若 ![]() ,求k的值;
,求k的值;
(Ⅱ)求四边形AEBF面积的最大值.
【答案】解:(Ⅰ)依题设得椭圆的方程为 ![]() ,
,
直线AB,EF的方程分别为x+2y=2,y=kx(k>0).
如图,
设D(x0 , kx0),E(x1 , kx1),F(x2 , kx2),其中x1<x2 ,
且x1 , x2满足方程(1+4k2)x2=4,
故 ![]() .①
.①
由 ![]() 知x0﹣x1=6(x2﹣x0),得
知x0﹣x1=6(x2﹣x0),得 ![]() ;
;
由D在AB上知x0+2kx0=2,得 ![]() .
.
所以 ![]() ,
,
化简得24k2﹣25k+6=0,
解得 ![]() 或
或 ![]() .
.
(Ⅱ)由题设,|BO|=1,|AO|=2.由(Ⅰ)知,E(x1 , kx1),F(x2 , kx2),
不妨设y1=kx1 , y2=kx2 , 由①得x2>0,根据E与F关于原点对称可知y2=﹣y1>0,
故四边形AEBF的面积为S=S△OBE+S△OBF+S△OAE+S△OAF
= ![]() (﹣y1)
(﹣y1)
= ![]()
=x2+2y2
= ![]() =
= ![]() =
= ![]() ,
,
当x2=2y2时,上式取等号.所以S的最大值为 ![]()
【解析】(1)依题可得椭圆的方程,设直线AB,EF的方程分别为x+2y=2,y=kx,D(x0 , kx0),E(x1 , kx1),F(x2 , kx2),且x1 , x2满足方程(1+4k2)x2=4,进而求得x2的表达式,进而根据 ![]() 求得x0的表达式,由D在AB上知x0+2kx0=2,进而求得x0的另一个表达式,两个表达式相等求得k.(Ⅱ)由题设可知|BO|和|AO|的值,设y1=kx1 , y2=kx2 , 进而可表示出四边形AEBF的面积进而根据基本不等式的性质求得最大值.
求得x0的表达式,由D在AB上知x0+2kx0=2,进而求得x0的另一个表达式,两个表达式相等求得k.(Ⅱ)由题设可知|BO|和|AO|的值,设y1=kx1 , y2=kx2 , 进而可表示出四边形AEBF的面积进而根据基本不等式的性质求得最大值.
【考点精析】通过灵活运用向量的共线定理,掌握设![]() ,
,![]() ,其中
,其中![]() ,则当且仅当
,则当且仅当![]() 时,向量
时,向量![]() 、
、![]() 共线即可以解答此题.
共线即可以解答此题.


科目:高中数学 来源: 题型:
【题目】a,b为正数,给出下列命题:
①若a2﹣b2=1,则a﹣b<1;
②若 ![]() ﹣
﹣ ![]() =1,则a﹣b<1;
=1,则a﹣b<1;
③ea﹣eb=1,则a﹣b<1;
④若lna﹣lnb=1,则a﹣b<1.
期中真命题的有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来蓬勃发展新机遇,2016年双11期间,某网络购物平台推销了A,B,C三种商品,某网购者决定抢购这三种商品,假设该名网购者都参与了A,B,C三种商品的抢购,抢购成功与否相互独立,且不重复抢购同一种商品,对A,B,C三件商品抢购成功的概率分别为a,b, ![]() ,已知三件商品都被抢购成功的概率为
,已知三件商品都被抢购成功的概率为 ![]() ,至少有一件商品被抢购成功的概率为
,至少有一件商品被抢购成功的概率为 ![]() .
.
(1)求a,b的值;
(2)若购物平台准备对抢购成功的A,B,C三件商品进行优惠减免,A商品抢购成功减免2百元,B商品抢购成功减免4比百元,C商品抢购成功减免6百元.求该名网购者获得减免总金额(单位:百元)的分别列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角三角形ABC 中,角 A,B,C 的对边分别为 a,b,c.若a=2bsinC,则tanA+tanB+tanC的最小值是( )
A.4
B.![]()
C.8
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乐队参加一户外音乐节,准备从3首原创新曲和5首经典歌曲中随机选择4首进行演唱.
(1)求该乐队至少演唱1首原创新曲的概率;
(2)假定演唱一首原创新曲观众与乐队的互动指数为a(a为常数),演唱一首经典歌曲观众与乐队的互动指数为2a.求观众与乐队的互动指数之和 ![]() 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosx(sinx﹣cosx)+m(m∈R),将y=f(x)的图象向左平移 ![]() 个单位后得到y=g(x)的图象,且y=g(x)在区间
个单位后得到y=g(x)的图象,且y=g(x)在区间 ![]() 内的最大值为
内的最大值为 ![]() .
.
(1)求实数m的值;
(2)在△ABC中,内角A、B、C的对边分别是a、b、c,若 ![]() ,且a+c=2,求△ABC的周长l的取值范围.
,且a+c=2,求△ABC的周长l的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
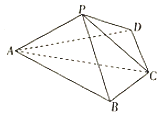
【题目】如图,四棱锥P﹣ABCD中,平面PAC⊥底面ABCD,BC=CD= ![]() AC=2,∠ACB=∠ACD=
AC=2,∠ACB=∠ACD= ![]() .
. 
(1)证明:AP⊥BD;
(2)若AP= ![]() ,AP与BC所成角的余弦值为
,AP与BC所成角的余弦值为 ![]() ,求二面角A﹣BP﹣C的余弦值..
,求二面角A﹣BP﹣C的余弦值..
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com