
①④
【解析】
试题分析:①f(x)=x2-x+1,g(x)=3x-2
设h(x)=f(x)-g(x)=x2-4x+3
h(x)在[1,2]上单调减,在[2,3]上单调增
∴h(x)的最大值为0,最小值为-1
∴对任意的x∈[1,3],都有|f(x)-g(x)|≤1,符合定义
②f(x)=x3+x,g(x)=3x2+x-1
设h(x)=f(x)-g(x)=x3+3x2+1
h′(x)=3x2+6x,x∈[1,3],h′(x)>0
h(x)在[1,3]上单调增
∴h(x)的最大值为55,最小值为5,
∴对任意的x∈[1,3],|f(x)-g(x)|≤1不成立,不符合定义
③f(x)=log2(x+1),g(x)=3-x
设h(x)=f(x)-g(x)=log2(x+1)+x-3
h(x)在[1,3]上单调增
∴h(x)的最大值为2,最小值为-1,
∴对任意的x∈[1,3],|f(x)-g(x)|≤1不成立,不符合定义
④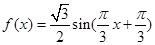 ,
, 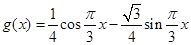
设h(x)=f(x)-g(x)=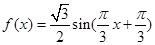 -(
-(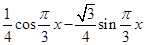 )=
)=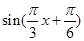
∵x∈[1,3],∴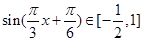
∴对任意的x∈[1,3],都有|f(x)-g(x)|≤1,符合定义
故答案为:①④
考点:本题主要考查了新定义题,主要涉及了函数的单调性,函数的最值求法等,同时考查计算能力,属于中档题
点评:解决该试题的关键是对照新定义,构造新函数h(x)=f(x)-g(x),利用导数的方法确定函数的单调性,从而确定函数的值域,利用若对任意的x∈D,都有|f(x)-g(x)|≤1,则称f(x)和g(x)在D上是“密切函数”,即可得到结论


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:高中数学 来源: 题型:
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 4 |
| π |
| 3 |
| ||
| 4 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2x |
| x+2 |
| 2 |
| 3 |
| 5 |
| 8 |
| x |
查看答案和解析>>
科目:高中数学 来源:2010年高考试题(福建卷)解析版(理) 题型:选择题
对于具有相同定义域D的函数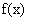 和
和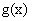 ,若存在函数
,若存在函数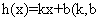 为常数),对任给的正数m,存在相应的
为常数),对任给的正数m,存在相应的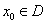 ,使得当
,使得当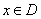 且
且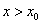 时,总有
时,总有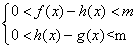 ,则称直线
,则称直线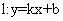 为曲线
为曲线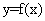 和
和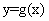 的“分渐近线”.给出定义域均为D=
的“分渐近线”.给出定义域均为D=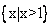 的四组函数如下:
的四组函数如下:
① ,
,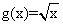 ; ②
; ② ,
,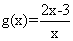 ;
;
③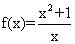 ,
,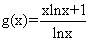 ;
④
;
④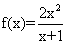 ,
,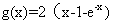 .
.
其中,
曲线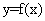 和
和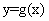 存在“分渐近线”的是( )
存在“分渐近线”的是( )
A. ①④ B. ②③ C.②④ D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com