
| 4 |
| x |
| x | … |
|
|
1 |
|
2 |
|
4 | 8 | 16 | … | ||||||||
| y | … | 16.25 | 8.5 | 5 |
|
4 |
|
5 | 8.5 | 16.25 | … |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |


 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2011 |
| 2 |
| 2011 |
| 3 |
| 2011 |
| 4 |
| 2011 |
| 2010 |
| 2011 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某同学探究函数 (x>0)的最小值,并确定相应的x的值.先列表如下:
(x>0)的最小值,并确定相应的x的值.先列表如下:
| x | … |  |  | 1 |  | 2 |  | 4 | 8 | 16 | … |
| y | … | 16.25 | 8.5 | 5 |  | 4 |  | 5 | 8.5 | 16.25 | … |
请观察表中y值随x值变化的特点,完成下列问题:((1)(2)问的填空只要写出结果即可)
(1)若x1x2=4,则 f(x1)______f(x2).(请填写“>,=,<”号);若函数 (x>0)在区间 (0,2)上递减,则f(x)在区间______ 上递增;
(x>0)在区间 (0,2)上递减,则f(x)在区间______ 上递增;
(2)当x=______时, (x>0)的最小值为______;
(x>0)的最小值为______;
(3)根据函数f(x)的有关性质,你能得到函数 (x<0)的最大值吗?为什么?
(x<0)的最大值吗?为什么?
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 4 |
| x |
| x | … |
|
|
1 |
|
2 |
|
4 | 8 | 16 | … | ||||||||
| y | … | 16.25 | 8.5 | 5 |
|
4 |
|
5 | 8.5 | 16.25 | … |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年贵州省贵阳市普通中学高一(上)期末数学试卷(解析版) 题型:解答题
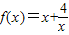 (x>0)的最小值,并确定相应的x的值.先列表如下:
(x>0)的最小值,并确定相应的x的值.先列表如下:| x | … |  |  | 1 |  | 2 |  | 4 | 8 | 16 | … |
| y | … | 16.25 | 8.5 | 5 | 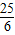 | 4 | 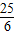 | 5 | 8.5 | 16.25 | … |
 (x>0)在区间 (0,2)上递减,则f(x)在区间______ 上递增;
(x>0)在区间 (0,2)上递减,则f(x)在区间______ 上递增;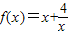 (x>0)的最小值为______;
(x>0)的最小值为______;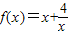 (x<0)的最大值吗?为什么?
(x<0)的最大值吗?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com