Question

若一个动点P（x,y）到两个定点A（-1，0），A′（1,0）的距离和为定值m，试求P点的轨迹方程.

Answer 1

思路分析：对m的值分类讨论，m＞2时利用椭圆定义求解；m=2时，P点轨迹为线段；m＜2时无图形.

解：∵|PA|+|PA′|=m,|AA′|=2，|PA|+|PA′|≥|AA′|，∴m≥2.?

（1）当m=2时，P点的轨迹就是线段AA′.?

∴其方程为y=0（-1≤x≤1）.?

（2）当m＞2时，由椭圆的定义知，点P的轨迹是以A、A′为焦点的椭圆.?

∵2c=2,2a=m,?

∴a=,c=1,b²=a²-c²=1.

∴点P的轨迹方程为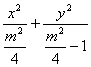=1.

温馨提示

平面内一动点到两定点的距离和等于常数时，动点的轨迹不一定是椭圆.当动点到两定点的距离和等于两定点之间的距离时，动点的轨迹是线段；当动点到两定点的距离和（常数）大于两定点之间的距离时，动点的轨迹是椭圆.