
解:(1)在平面直角坐标系中,已知P1(x1,y1),P2(x2,y2),则|P1P2|=![]() .?
.?
(2)在空间直角坐标系中,?
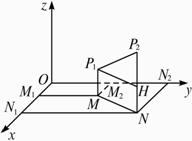
如图,设P1(x1,y1,z1)、P2(x2,y2,z2)是空间中任意两点,且点P1(x1,y1,z1)、P2(x2,y2,z2)在xOy平面上的射影分别为M、N,那么M、N的坐标为M(x1,y1,0)、N(x2,y2,0),在xOy平面上,|MN|=![]() .?
.?
过点P1作P2N的垂线,垂足为H,则|MP1|=|z1|,|NP2|=|z2|,所以|HP2|=|z2-z1|.?
在Rt△P1HP2中,|P1H|=|MN|=![]() ,根据勾股定理,得?
,根据勾股定理,得?
|P1P2|=![]() =
=![]() .?
.?
因此,空间中点P1(x1,y1,z1),P2(x2,y2,z2)之间的距离?
|P1P2|=![]() .?
.?
(3)我们来确定P1、P2两点在柱坐标系中的距离公式:?
根据空间点P的直角坐标(x,y,z)与柱坐标(ρ,θ,z)之间的变换公式: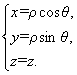
P1(x1,y1,z1),P2(x2,y2,z2),有
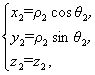 可得|P1P2|=
可得|P1P2|=![]()
(4)我们来确定P1、P2两点在球坐标系中的距离公式:?
空间点P的直角坐标(x,y,z)与球坐标(r,φ,θ)之间的变换关系为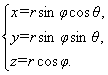
P1(x1,y1,z1),P2(x2,y2,z2),有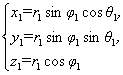 及
及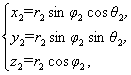
可得|P1P2|=![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(08年荆州市质检二) (12分) 如图是两个独立的转盘![]() ,在两个图中三个扇形区域的圆心角分别为
,在两个图中三个扇形区域的圆心角分别为![]() 。用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘
。用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘![]() 指针所对的区域数为
指针所对的区域数为![]() ,转盘
,转盘![]() 指针所对的区域为
指针所对的区域为![]() ,
,![]() ,设
,设![]() 的值为
的值为![]() ,每一次游戏得到奖励分为
,每一次游戏得到奖励分为![]()
⑴求![]() 且
且![]() 的概率;
的概率;
⑵某人进行了![]() 次游戏,求他平均可以得到的奖励分
次游戏,求他平均可以得到的奖励分
(注:这是一个几何概率题,几何概率的基本思想是把事件与几何区域对应,利用几何区域的度量来计算事件发生的概率,即事件![]() 的概率
的概率![]() )
)

查看答案和解析>>
科目:高中数学 来源: 题型:
如图是两个独立的转盘![]() ,在两个图中三个扇形区域的圆心角分别为
,在两个图中三个扇形区域的圆心角分别为![]() 。用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘
。用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘![]() 指针所对的区域数为
指针所对的区域数为![]() ,转盘
,转盘![]() 指针所对的区域为
指针所对的区域为![]() ,
,![]() ,设
,设![]() 的值为
的值为![]() ,每一次游戏得到奖励分为
,每一次游戏得到奖励分为![]()

⑴求![]() 且
且![]() 的概率;
的概率;
⑵某人进行了![]() 次游戏,求他平均可以得到的奖励分
次游戏,求他平均可以得到的奖励分
(注:这是一个几何概率题,几何概率的基本思想是把事件与几何区域对应,利用几何区域的度量来计算事件发生的概率,即事件![]() 的概率
的概率![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com