
【题目】定义域为R的偶函数f(x)满足对x∈R,有f(x+2)=f(x)﹣f(1),且当x∈[2,3]时,f(x)=﹣2x2+12x﹣18,若函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,则a的取值范围是 .
【答案】(0, ![]() )
)
【解析】解:∵f(x+2)=f(x)﹣f(1),
且f(x)是定义域为R的偶函数,
令x=﹣1可得f(﹣1+2)=f(﹣1)﹣f(1),
又f(﹣1)=f(1),
∴f(1)=0 则有f(x+2)=f(x),
∴f(x)是最小正周期为2的偶函数.
当x∈[2,3]时,f(x)=﹣2x2+12x﹣18=﹣2(x﹣3)2 ,
函数的图象为开口向下、顶点为(3,0)的抛物线.
∵函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,
令g(x)=loga(|x|+1),则f(x)的图象和g(x)的图象至少有3个交点.
∵f(x)≤0,∴g(x)≤0,可得0<a<1,
要使函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,
则有g(2)>f(2),可得 loga(2+1)>f(2)=﹣2,
即loga3>﹣2,∴3< ![]() ,解得-
,解得- ![]() <a<
<a< ![]() ,又0<a<1,∴0<a<
,又0<a<1,∴0<a< ![]() ,
,
故答案为:(0, ![]() ).
).
令x=﹣1,求出f(1),可得函数f(x)的周期为2,当x∈[2,3]时,f(x)=﹣2x2+12x﹣18,画出图形,根据函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,利用数形结合的方法进行求解.


科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出![]() 盒该产品获利润
盒该产品获利润![]() 元;未售出的产品,每盒亏损
元;未售出的产品,每盒亏损![]() 元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示。该同学为这个开学季购进了
元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示。该同学为这个开学季购进了![]() 盒该产品,以
盒该产品,以![]() (单位:盒,
(单位:盒,![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量,![]() (单位:元)表示这个开学季内经销该产品的利润。
(单位:元)表示这个开学季内经销该产品的利润。

(1)求市场需求量在[100,120]的概率;
(2)根据直方图估计这个开学季内市场需求量![]() 的中位数;
的中位数;
(3)将![]() 表示为
表示为![]() 的函数,并根据直方图估计利润不少于
的函数,并根据直方图估计利润不少于![]() 元的概率。
元的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D. 
(1)求证:CE2=CDCB.
(2)若AB=2,BC= ![]() ,求CE与CD的长.
,求CE与CD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)=(|x﹣2|+1)4,给出如下三个命题:①f(x+2)是偶函数;②f(x)在区间(﹣∞,2)上是减函数,在区间(2,+∞)上是增函数;③f(x)没有最小值.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,∠BCA=90°,M、N分别是A1B1、A1C1的中点,BC=AC=CC1 , 则CN与AM所成角的余弦值等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位安排![]() 位员工在春节期间大年初一到初七值班,每人值班
位员工在春节期间大年初一到初七值班,每人值班![]() 天,若
天,若![]() 位员工中的甲、乙排在相邻的两天,丙不排在初一,丁不排在初七,则不同的安排方案共有( )
位员工中的甲、乙排在相邻的两天,丙不排在初一,丁不排在初七,则不同的安排方案共有( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,等比数列
,等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)若![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)21或
;(2)21或![]() .
.
【解析】试题分析:(1)设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() ,由已知条件求出
,由已知条件求出![]() ,再写出通项公式;(2)由
,再写出通项公式;(2)由![]() ,求出
,求出![]() 的值,再求出
的值,再求出![]() 的值,求出
的值,求出![]() 。
。
试题解析:设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() 有
有![]() ,即
,即![]() .
.
(1)∵![]() ,结合
,结合![]() 得
得![]() ,
,
∴![]() .
.
(2)∵![]() ,解得
,解得![]() 或3,
或3,
当![]() 时,
时,![]() ,此时
,此时![]() ;
;
当![]() 时,
时,![]() ,此时
,此时![]() .
.
【题型】解答题
【结束】
20
【题目】如图,已知直线与抛物线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,
, ![]() 交
交![]() 于
于![]() ,且点
,且点![]() 的坐标为
的坐标为![]() .
.
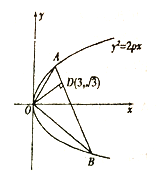
(1)求![]() 的值;
的值;
(2)若![]() 为抛物线的焦点,
为抛物线的焦点, ![]() 为抛物线上任一点,求
为抛物线上任一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com