练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （1+tan21°）（1+tan22°）（1+tan23°）（1+tan24°）的值是     ．
    【答案】分析：由tan45°=tan（21°+24°）=tan（22°+23°）利用两角和的正切函数公式化简得到①②，把原式的一四项结合，二三项结合分别化简后，将①②代入即可求出．
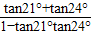
    解答：解：根据tan45°=tan（21°+24°）==1
    得到tan21°+tan24°=1-tan21°tan24°①；同理得到tan22°+tan23°=1-tan22°tan23°②；
    则原式=[（1+tan21°）（1+tan24°）][（1+tan22°）（1+tan23°）]
    =（1+tan24°+tan21°+tan24°tan21°）（1+tan22°+tan23°+tan22°tan23°）
    =（1+1-tan24°tan21°+tan24°tan21°）（1+1-tan22°tan23°+tan22°tan23°）=4
    故答案为：4．
    点评：此题的突破点是角度的变化即利用45°=21°+24°=22°+23°化简求值，要求学生会灵活运用两角和与差的正切函数公式化简求值．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

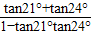    科目：高中数学 来源： 题型：013

    (1+tan21°)(1+tan22°)(1+tan23°)(1+tan24°)的值是(　　 ) 

    A.16　　　　　　　　　　　　      　B.8　　　　　　　　　　 　　C.4  　　　　　　　　　　  　　  D.2 

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：013

    (1+tan21°)(1+tan22°)(1+tan23°)(1+tan24°)的值是(　　 ) 

    A.16　　　　　　　　　　　　      　B.8　　　　　　　　　　 　　C.4  　　　　　　　　　　  　　  D.2 

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (1+tan21°)(1+tan20°)(1+tan25°)(1+tan24°)的值是(    )

    A．2         B．4          C．8            D．16

    查看答案和解析>>

    同步练习册答案