
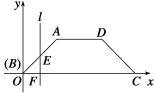
【题目】如图所示,已知底角为45°的等腰梯形ABCD,底边BC长为7 cm,腰长为2![]() cm,当一条垂直于底边BC(垂足为F)的直线l从B点开始由左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x(0≤x≤7),左边部分的面积为y,求y与x之间的函数关系式,画出程序框图,并写出程序.
cm,当一条垂直于底边BC(垂足为F)的直线l从B点开始由左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x(0≤x≤7),左边部分的面积为y,求y与x之间的函数关系式,画出程序框图,并写出程序.
【答案】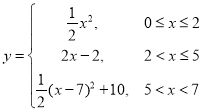 ,程序框图和程序见解析.
,程序框图和程序见解析.
【解析】
根据直线![]() 将梯形分割的左边部分的形状进行分类讨论,求出函数关系式,即可根据条件结构画出程序框图,并写出程序.
将梯形分割的左边部分的形状进行分类讨论,求出函数关系式,即可根据条件结构画出程序框图,并写出程序.
过点A,D分别作AG⊥BC,DH⊥BC,垂足分别是G,H.
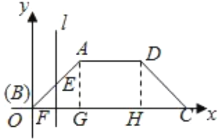
∵四边形ABCD是等腰梯形,底角是45°,AB=2cm,
∴BG=AG=DH=HC=2 cm.
又BC=7cm,∴AD=GH=3cm,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
所以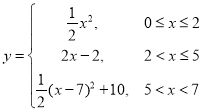 .
.
程序框图如下:
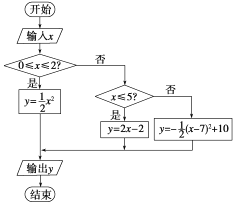
程序:
INPUT“x=”;x
IF x>=0 AND x<=2 THEN
y=0.5 *x^2
ELSE
IF x<=5 THEN
y=2*x-2
ELSE
y =-0.5*(x-7) ^2+10
END IF
END IF
PRINT y
END


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知曲线C:y=![]() ,D为直线y=
,D为直线y=![]() 上的动点,过D作C的两条切线,切点分别为A,B.
上的动点,过D作C的两条切线,切点分别为A,B.
(1)证明:直线AB过定点:
(2)若以E(0,![]() )为圆心的圆与直线AB相切,且切点为线段AB的中点,求四边形ADBE的面积.
)为圆心的圆与直线AB相切,且切点为线段AB的中点,求四边形ADBE的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
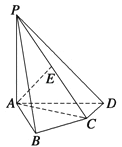
(1)求PB和平面PAD所成的角的大小;
(2)证明AE⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 分别是椭圆
分别是椭圆![]()
![]() 的左、右焦点,过
的左、右焦点,过![]() 与
与![]() 轴垂直的直线交椭圆于点
轴垂直的直线交椭圆于点![]() ,且
,且![]()
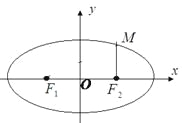
(1)求椭圆的标准方程;
(2)已知点![]() ,问是否存在直线
,问是否存在直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,
,![]() ,且
,且![]() 的垂直平分线恰好过
的垂直平分线恰好过![]() 点?若存在,求出直线
点?若存在,求出直线![]() 斜率的取值范围;若不存在,请说明理由.
斜率的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P—ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.
(Ⅰ)求证:BE∥平面PAD;
(Ⅱ)求证:BC⊥平面PBD;
(Ⅲ)设Q为侧棱PC上一点,![]() 试确定
试确定![]() 的值,使得二面角Q—BD—P为45°.
的值,使得二面角Q—BD—P为45°.
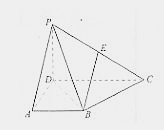
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题,其中正确命题有( )
A.空间任意三个不共面的向量都可以作为一个基底
B.已知向量![]() ,则
,则![]() 与任何向量都不能构成空间的一个基底
与任何向量都不能构成空间的一个基底
C.![]() 是空间四点,若
是空间四点,若![]() 不能构成空间的一个基底,那么
不能构成空间的一个基底,那么![]() 共面
共面
D.已知向量![]() 组是空间的一个基底,若
组是空间的一个基底,若![]() ,则
,则![]() 也是空间的一个基底
也是空间的一个基底
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com