
【题目】已知曲线C:y=![]() ,D为直线y=
,D为直线y=![]() 上的动点,过D作C的两条切线,切点分别为A,B.
上的动点,过D作C的两条切线,切点分别为A,B.
(1)证明:直线AB过定点:
(2)若以E(0,![]() )为圆心的圆与直线AB相切,且切点为线段AB的中点,求四边形ADBE的面积.
)为圆心的圆与直线AB相切,且切点为线段AB的中点,求四边形ADBE的面积.
【答案】(1)见详解;(2) 3或![]() .
.
【解析】
可用解析法和几何法证明。解析法可设A,B两点的坐标分别为![]() ,
,![]() ,然后求出A,B两点处的切线,两条切线交于直线
,然后求出A,B两点处的切线,两条切线交于直线![]() 之上,所以交点的纵坐标为
之上,所以交点的纵坐标为![]()
联立方程可解![]() 和
和![]() 的关系。之后用两点式求出直线
的关系。之后用两点式求出直线![]() 方程,最后根据直线
方程,最后根据直线![]() 方程求出它所过的定点.(2)应用四边形面积公式,代入化简出关于
方程求出它所过的定点.(2)应用四边形面积公式,代入化简出关于![]() 和
和![]() 的对称式。然后分情况讨论求解。如果不知道四面下面积公式则可以将四边形分成两个三角形求面积之后做和,但会稍微麻烦一些。(此题若用向量积的概念则更为容易)
的对称式。然后分情况讨论求解。如果不知道四面下面积公式则可以将四边形分成两个三角形求面积之后做和,但会稍微麻烦一些。(此题若用向量积的概念则更为容易)
(1)证明:设A,B两点的坐标分别为![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
则切线DA为:![]() ---------①,切线DB为:
---------①,切线DB为:![]() --------②,
--------②,
代入![]() 得
得 ,
,![]() 得
得![]() ,因为
,因为![]() 故消去得交点的纵坐标
故消去得交点的纵坐标![]() ,
,
因为DA和DB的交点D为直线![]() 上的动点,所以有
上的动点,所以有![]() ,
,![]() ,
,
直线AB为![]() ,点A,B在曲线
,点A,B在曲线![]() 上,则有
上,则有 ,整理得
,整理得![]() ,即
,即![]() .当
.当![]() ,
,![]() 时无论
时无论![]() ,
,![]() 取何值时,此等式均成立。因此直线AB过定点
取何值时,此等式均成立。因此直线AB过定点![]() ,得证。
,得证。
(2)设AB的中点为G,由题得G点坐标为![]() ,则
,则![]() ,又
,又![]() .由题意知
.由题意知![]() ,即
,即![]() 即
即![]() .代入
.代入![]() 得
得![]() 整理得
整理得![]() .
.
因![]() ,故
,故![]() .所以
.所以![]() 或
或![]() .
.
由第一问中 ,为这里的
,为这里的![]() 为D点坐标,然而
为D点坐标,然而![]() ,故
,故
![]() ,所以
,所以![]() ,又因为
,又因为![]() .所以
.所以![]() 。即D坐标为
。即D坐标为![]() .
.
那么![]() ,
,![]() .
.
设![]() 为
为![]() 与
与![]() 的夹角,那么有
的夹角,那么有

代入![]() 进行化简有
进行化简有![]()
若![]() ,则
,则![]() .
.
若![]() ,则
,则![]() ,
,![]()
代入有![]() .
.
所以四边形ADBE的面积为3或![]() .
.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】 设椭圆![]() 的左焦点为
的左焦点为![]() ,左顶点为
,左顶点为![]() ,顶点为B.已知
,顶点为B.已知![]() (
(![]() 为原点).
为原点).
(Ⅰ)求椭圆的离心率;
(Ⅱ)设经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆在
与椭圆在![]() 轴上方的交点为
轴上方的交点为![]() ,圆
,圆![]() 同时与
同时与![]() 轴和直线
轴和直线![]() 相切,圆心
相切,圆心![]() 在直线
在直线![]() 上,且
上,且![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-![]() 中,
中,![]() 平面ABC,D,E,F,G分别为
平面ABC,D,E,F,G分别为![]() ,AC,
,AC,![]() ,
,![]() 的中点,AB=BC=
的中点,AB=BC=![]() ,AC=
,AC=![]() =2.
=2.

(Ⅰ)求证:AC⊥平面BEF;
(Ⅱ)求二面角B-CD-C1的余弦值;
(Ⅲ)证明:直线FG与平面BCD相交.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”;
”;
②“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
③![]() 命题“,使得
命题“,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”;
”;
④命题“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
其中所有正确命题的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,![]() 是锐角,大小为β.图中阴影区域的面积的最大值为
是锐角,大小为β.图中阴影区域的面积的最大值为
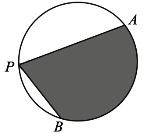
A. 4β+4cosβB. 4β+4sinβC. 2β+2cosβD. 2β+2sinβ
查看答案和解析>>
科目:高中数学 来源: 题型:
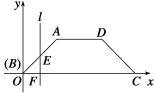
【题目】如图所示,已知底角为45°的等腰梯形ABCD,底边BC长为7 cm,腰长为2![]() cm,当一条垂直于底边BC(垂足为F)的直线l从B点开始由左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x(0≤x≤7),左边部分的面积为y,求y与x之间的函数关系式,画出程序框图,并写出程序.
cm,当一条垂直于底边BC(垂足为F)的直线l从B点开始由左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x(0≤x≤7),左边部分的面积为y,求y与x之间的函数关系式,画出程序框图,并写出程序.
查看答案和解析>>
科目:高中数学 来源: 题型:
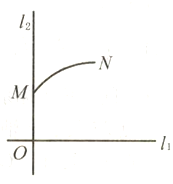
【题目】如图,![]() ,
,![]() 分别是通过某城市开发区中心O的两条东西和南北走向的街道,连接M,N两地间的铁路是圆心在
分别是通过某城市开发区中心O的两条东西和南北走向的街道,连接M,N两地间的铁路是圆心在![]() 上的一段圆弧.若点M在点O正北方向,且
上的一段圆弧.若点M在点O正北方向,且![]() ,点N到
,点N到![]() ,
,![]() 的距离分别为5km和4km.
的距离分别为5km和4km.
(1)建立适当的坐标系,求铁路路线所在圆弧的方程.
(2)若该城市的某中学拟在点O正东方向选址建分校,考虑环境问题,要求校址到点O的距离大于4km,并且铁路上任意一点到校址的距离不能小于![]() km,求该校址距点O的最近距离.
km,求该校址距点O的最近距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com