
【题目】 设椭圆![]() 的左焦点为
的左焦点为![]() ,左顶点为
,左顶点为![]() ,顶点为B.已知
,顶点为B.已知![]() (
(![]() 为原点).
为原点).
(Ⅰ)求椭圆的离心率;
(Ⅱ)设经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆在
与椭圆在![]() 轴上方的交点为
轴上方的交点为![]() ,圆
,圆![]() 同时与
同时与![]() 轴和直线
轴和直线![]() 相切,圆心
相切,圆心![]() 在直线
在直线![]() 上,且
上,且![]() ,求椭圆的方程.
,求椭圆的方程.
【答案】(I)首先设椭圆的半焦距为![]() ,根据题意得到
,根据题意得到![]() ,结合椭圆中
,结合椭圆中![]() 的关系,得到
的关系,得到![]() ,化简得出
,化简得出![]() ,从而求得其离心率;
,从而求得其离心率;
(II)结合(I)的结论,设出椭圆的方程![]() ,写出直线的方程,两个方程联立,求得交点的坐标,利用直线与圆相切的条件,列出等量关系式,求得
,写出直线的方程,两个方程联立,求得交点的坐标,利用直线与圆相切的条件,列出等量关系式,求得![]() ,从而得到椭圆的方程.
,从而得到椭圆的方程.
【解析】
(I)![]() ;
;
(II)![]() .
.
(I)解:设椭圆的半焦距为![]() ,由已知有
,由已知有![]() ,
,
又由![]() ,消去
,消去![]() 得
得![]() ,解得
,解得![]() ,
,
所以,椭圆的离心率为![]() .
.
(II)解:由(I)知,![]() ,故椭圆方程为
,故椭圆方程为![]() ,
,
由题意,![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
点![]() 的坐标满足
的坐标满足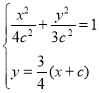 ,消去
,消去![]() 并化简,得到
并化简,得到![]() ,
,
解得![]() ,
,
代入到![]() 的方程,解得
的方程,解得![]() ,
,
因为点![]() 在
在![]() 轴的上方,所以
轴的上方,所以![]() ,
,
由圆心在直线![]() 上,可设
上,可设![]() ,因为
,因为![]() ,
,
且由(I)知![]() ,故
,故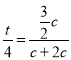 ,解得
,解得![]() ,
,
因为圆![]() 与
与![]() 轴相切,所以圆的半径为2,
轴相切,所以圆的半径为2,
又由圆![]() 与
与![]() 相切,得
相切,得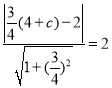 ,解得
,解得![]() ,
,
所以椭圆的方程为:![]() .
.


科目:高中数学 来源: 题型:
【题目】给出如下四个命题:
①“![]() ”是“
”是“![]() ”的充分而不必要条件;
”的充分而不必要条件;
②命题“若![]() ,则函数
,则函数![]() 有一个零点”的逆命题为真命题;
有一个零点”的逆命题为真命题;
③若![]() 是
是![]() 的必要条件,则
的必要条件,则![]() 是
是![]() 的充分条件;
的充分条件;
④在![]() 中,“
中,“![]() ”是“
”是“![]() ”的既不充分也不必要条件.
”的既不充分也不必要条件.
其中正确的命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,若存在闭区间
,若存在闭区间![]() ,使得函数
,使得函数![]() 满足:①
满足:①![]() 在
在![]()
上是单调函数;②![]() 在
在 ![]() 上的值域是
上的值域是![]() ,则称区间
,则称区间![]() 是函数
是函数 ![]() 的“和谐区间”,
的“和谐区间”,
下列结论错误的是( )
A.函数 ![]() 存在 “和谐区间”
存在 “和谐区间”
B.函数 ![]() 存在 “和谐区间”
存在 “和谐区间”
C.函数 ![]() 不存在 “和谐区间”
不存在 “和谐区间”
D.函数 ![]() 存在 “和谐区间”
存在 “和谐区间”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量按照其质量指标值M进行等级划分,具体如下表:
质量指标值M |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
现从某企业生产的这种产品中随机抽取了100件作为样本,对其质量指标值M进行统计分析,得到如图所示的频率分布直方图.
(1)记A表示事件“一件这种产品为二等品或一等品”,试估计事件A的概率;
(2)已知该企业的这种产品每件一等品、二等品、三等品的利润分别为10元、6元、2元,试估计该企业销售10000件该产品的利润;
(3)根据该产品质量指标值M的频率分布直方图,求质量指标值M的中位数的估计值(精确到0.01)
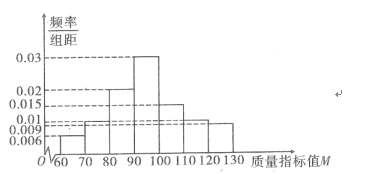
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区甲、乙、丙三所单位进行招聘,其中甲单位招聘2名,乙单位招聘2名,丙单位招聘1名,并且甲单位要至少招聘一名男生,现有3男3女参加三所单位的招聘,则不同的录取方案种数为( )
A.36B.72C.108D.144
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的极值;
的极值;
(2)是否存在实数![]() ,使得
,使得![]() 与
与![]() 的单调区间相同,若存在,求出
的单调区间相同,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)若![]() ,求证:
,求证:![]() 在
在![]() 上恒成立.
上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研团队对某一生物生长规律进行研究,发现其生长蔓延的速度越来越快.开始在某水域投放一定面积的该生物,经过2个月其覆盖面积为18平方米,经过3个月其覆盖面积达到27平方米.该生物覆盖面积![]() (单位:平方米)与经过时间
(单位:平方米)与经过时间![]() 个月的关系有两个函数模型
个月的关系有两个函数模型![]() 与
与![]() 可供选择.
可供选择.
(1)试判断哪个函数模型更合适,并求出该模型的函数解析式;
(2)问约经过几个月,该水域中此生物的面积是当初投放的1000倍![]() (参考数据:
(参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com