
【题目】某科研团队对某一生物生长规律进行研究,发现其生长蔓延的速度越来越快.开始在某水域投放一定面积的该生物,经过2个月其覆盖面积为18平方米,经过3个月其覆盖面积达到27平方米.该生物覆盖面积![]() (单位:平方米)与经过时间
(单位:平方米)与经过时间![]() 个月的关系有两个函数模型
个月的关系有两个函数模型![]() 与
与![]() 可供选择.
可供选择.
(1)试判断哪个函数模型更合适,并求出该模型的函数解析式;
(2)问约经过几个月,该水域中此生物的面积是当初投放的1000倍![]() (参考数据:
(参考数据:![]() )
)
【答案】(1)答案见解析(2)![]()
【解析】
(1)因为函数![]() 中,
中,![]() 随
随![]() 的增长而增长的速度越来越快,而函数
的增长而增长的速度越来越快,而函数![]() 中,
中,![]() 随
随![]() 的增长而增长的速度越来越慢,根据已知条件应选
的增长而增长的速度越来越慢,根据已知条件应选![]() 更合适,结合已知,即可求得该模型的函数解析式;
更合适,结合已知,即可求得该模型的函数解析式;
(2)由(Ⅰ)知,当![]() 时,
时,![]() ,所以原先投放的此生物的面积为8平方米,设经过
,所以原先投放的此生物的面积为8平方米,设经过![]() 个月该水域中此生物的面积是当初投放的1000倍,则有
个月该水域中此生物的面积是当初投放的1000倍,则有![]() ,即可求得答案.
,即可求得答案.
(1)![]() 函数
函数![]() 中,
中,![]() 随
随![]() 的增长而增长的速度越来越快,
的增长而增长的速度越来越快,
而函数![]() 中,
中,![]() 随
随![]() 的增长而增长的速度越来越慢,
的增长而增长的速度越来越慢,
根据已知条件应选![]() 更合适
更合适
由已知得 ,解得
,解得![]()
![]() 函数解析式为
函数解析式为
(2)由(1)知,当![]() 时,
时,![]() ,所以原先投放的此生物的面积为8平方米;
,所以原先投放的此生物的面积为8平方米;
设经过![]() 个月该水域中此生物的面积是当初投放的1000倍,
个月该水域中此生物的面积是当初投放的1000倍,
![]() 有
有![]()
解得![]()
![]() 约经过
约经过![]() 个月,该水域中此生物的面积是当初投放的1000倍.
个月,该水域中此生物的面积是当初投放的1000倍.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
【题目】 设椭圆![]() 的左焦点为
的左焦点为![]() ,左顶点为
,左顶点为![]() ,顶点为B.已知
,顶点为B.已知![]() (
(![]() 为原点).
为原点).
(Ⅰ)求椭圆的离心率;
(Ⅱ)设经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆在
与椭圆在![]() 轴上方的交点为
轴上方的交点为![]() ,圆
,圆![]() 同时与
同时与![]() 轴和直线
轴和直线![]() 相切,圆心
相切,圆心![]() 在直线
在直线![]() 上,且
上,且![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年春节期间,我国高速公路继续执行“节假日高速公路免费政策”某路桥公司为掌握春节期间车辆出行的高峰情况,在某高速公路收费点记录了大年初三上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如下图所示,其中时间段9:20~9:40记作区间![]() ,9:40~10:00记作
,9:40~10:00记作![]() ,10:00~10:20记作
,10:00~10:20记作![]() ,10:20~10:40记作
,10:20~10:40记作![]() .例如:10点04分,记作时刻64.
.例如:10点04分,记作时刻64.

(1)估计这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值(同一组中的数据用该组区间的中点值代表);
(2)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车中随机抽取4辆,设抽到的4辆车中,在9:20~10:00之间通过的车辆数为X,求X的分布列与数学期望;
(3)由大数据分析可知,车辆在每天通过该收费点的时刻T服从正态分布![]() ,其中
,其中![]() 可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,
可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,![]() 可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】浙江省现行的高考招生制度规定除语、数、英之外,考生须从政治、历史、地理、物理、化学、生物、技术这7门高中学考科目中选择3门作为高考选考科目,成绩计入高考总分.已知报考某高校![]() 、
、![]() 两个专业各需要一门科目满足要求即可,
两个专业各需要一门科目满足要求即可,![]() 专业:物理、化学、技术;
专业:物理、化学、技术;![]() 专业:历史、地理、技术.考生小李今年打算报考该高校这两个专业的选考方式有______ 种.(用数字作答)
专业:历史、地理、技术.考生小李今年打算报考该高校这两个专业的选考方式有______ 种.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若存在区间A=[m,n],使得{y|y=f(x),x∈A}=A,则称函数f(x)为“同域函数”,区间A为函数f(x)的一个“同域区间”.给出下列四个函数:
①![]() ;②f(x)=x2-1;③f(x)=|2x-1|;④f(x)=log2(x-1).
;②f(x)=x2-1;③f(x)=|2x-1|;④f(x)=log2(x-1).
存在“同域区间”的“同域函数”的序号是__________.(请写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() 同时满足:①对任意
同时满足:①对任意![]() ,都有
,都有![]() ;②当
;②当![]() 时,
时,![]() ,
,
(1)当![]() 时,求
时,求![]() 的表达式;
的表达式;
(2)若关于![]() 的方程
的方程![]() 在
在![]() 上有实数解,求实数
上有实数解,求实数![]() 的取值范围;
的取值范围;
(3)若对任意![]() ,关于
,关于![]() 的不等式
的不等式![]() 都成立,求实数
都成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将宽和长都分别为x,![]() 的两个矩形部分重叠放在一起后形成的正十字形面积为
的两个矩形部分重叠放在一起后形成的正十字形面积为![]() 注:正十字形指的是原来的两个矩形的顶点都在同一个圆上,且两矩形长所在的直线互相垂直的图形
注:正十字形指的是原来的两个矩形的顶点都在同一个圆上,且两矩形长所在的直线互相垂直的图形![]() ,
,
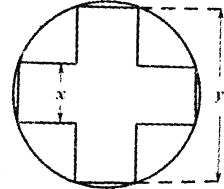
![]() 求y关于x的函数解析式;
求y关于x的函数解析式;
![]() 当x,y取何值时,该正十字形的外接圆面积最小,并求出其最小值.
当x,y取何值时,该正十字形的外接圆面积最小,并求出其最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com