
【题目】2019年春节期间,我国高速公路继续执行“节假日高速公路免费政策”某路桥公司为掌握春节期间车辆出行的高峰情况,在某高速公路收费点记录了大年初三上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如下图所示,其中时间段9:20~9:40记作区间![]() ,9:40~10:00记作
,9:40~10:00记作![]() ,10:00~10:20记作
,10:00~10:20记作![]() ,10:20~10:40记作
,10:20~10:40记作![]() .例如:10点04分,记作时刻64.
.例如:10点04分,记作时刻64.

(1)估计这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值(同一组中的数据用该组区间的中点值代表);
(2)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车中随机抽取4辆,设抽到的4辆车中,在9:20~10:00之间通过的车辆数为X,求X的分布列与数学期望;
(3)由大数据分析可知,车辆在每天通过该收费点的时刻T服从正态分布![]() ,其中
,其中![]() 可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,
可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,![]() 可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
【答案】(1)10点04分(2)分布列见解析,![]() (3)819辆
(3)819辆
【解析】
(1)利用频率分布直方图和平均数的计算公式,即可求得这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值;
(2)结合频率分布直方图和分层抽样的方法求得随机变量![]() 的可能取值
的可能取值![]() ,求出相应的概率,得到
,求出相应的概率,得到![]() 的分布列,利用期望的公式,求得其数学期望;
的分布列,利用期望的公式,求得其数学期望;
(3)由(1)可得![]() ,得到
,得到![]() ,得到概率,即可求解在9:46~10:40这一时间段内通过的车辆数.
,得到概率,即可求解在9:46~10:40这一时间段内通过的车辆数.
(1)由题意,这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值为
![]() ,即10点04分.
,即10点04分.
(2)结合频率分布直方图和分层抽样的方法可知:抽取的10辆车中,在10:00前通过的车辆数就是位于时间分组中在![]() 这一区间内的车辆数,即
这一区间内的车辆数,即![]() ,所以X的可能取值为0,1,2,3,1.
,所以X的可能取值为0,1,2,3,1.
所以![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以X的分布列为
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
所以![]() .
.
(3)由(1)可得![]() ,
,
![]() ,
,
所以![]() .
.
估计在9:46~10:40这一时间段内通过的车辆数,也就是![]() 通过的车辆数,
通过的车辆数,
由![]() ,
,
![]() ,
,
所以,估计在9:46~10:40这一时间段内通过的车辆数为![]() 辆.
辆.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,若存在闭区间
,若存在闭区间![]() ,使得函数
,使得函数![]() 满足:①
满足:①![]() 在
在![]()
上是单调函数;②![]() 在
在 ![]() 上的值域是
上的值域是![]() ,则称区间
,则称区间![]() 是函数
是函数 ![]() 的“和谐区间”,
的“和谐区间”,
下列结论错误的是( )
A.函数 ![]() 存在 “和谐区间”
存在 “和谐区间”
B.函数 ![]() 存在 “和谐区间”
存在 “和谐区间”
C.函数 ![]() 不存在 “和谐区间”
不存在 “和谐区间”
D.函数 ![]() 存在 “和谐区间”
存在 “和谐区间”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的极值;
的极值;
(2)是否存在实数![]() ,使得
,使得![]() 与
与![]() 的单调区间相同,若存在,求出
的单调区间相同,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)若![]() ,求证:
,求证:![]() 在
在![]() 上恒成立.
上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 具备以下两个条件:(1)至少有一条对称轴或一个对称中心;(2)至少有两个零点,则称这样的函数为“多元素”函数,下列函数中为“多元素”函数的是_______.
具备以下两个条件:(1)至少有一条对称轴或一个对称中心;(2)至少有两个零点,则称这样的函数为“多元素”函数,下列函数中为“多元素”函数的是_______.
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形PBCD中, ![]() ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将![]() 沿AB折到
沿AB折到![]() 的位置,使
的位置,使![]() ,点E在SD上,且
,点E在SD上,且![]() ,如下图。
,如下图。
(1)求证: ![]() 平面ABCD;
平面ABCD;
(2)求二面角E—AC—D的正切值.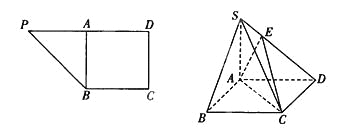
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研团队对某一生物生长规律进行研究,发现其生长蔓延的速度越来越快.开始在某水域投放一定面积的该生物,经过2个月其覆盖面积为18平方米,经过3个月其覆盖面积达到27平方米.该生物覆盖面积![]() (单位:平方米)与经过时间
(单位:平方米)与经过时间![]() 个月的关系有两个函数模型
个月的关系有两个函数模型![]() 与
与![]() 可供选择.
可供选择.
(1)试判断哪个函数模型更合适,并求出该模型的函数解析式;
(2)问约经过几个月,该水域中此生物的面积是当初投放的1000倍![]() (参考数据:
(参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com