
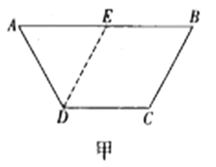
【题目】如图甲,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使二面角
折起,使二面角![]() 为
为![]() ,连接
,连接![]() ,
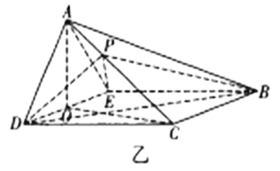
,![]() 得到四棱锥
得到四棱锥![]() (如图乙),
(如图乙),![]() 为
为![]() 的中点,
的中点,![]() 是棱
是棱![]() 上一点.
上一点.
(1)求证:当![]() 为
为![]() 的中点时,平面
的中点时,平面![]() 平面
平面![]() ;
;
(2)是否存在一点![]() ,使平面
,使平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,若存在,求
,若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)证明见解析(2)存在;![]()
【解析】
(1)由题易证得![]() ,根据等腰三角形的性质可得
,根据等腰三角形的性质可得![]() ,
,![]() ,则
,则![]() 平面
平面![]() ,由平行线的性质可知
,由平行线的性质可知![]() 平面
平面![]() ,则
,则![]() ,再利用
,再利用![]() 可得
可得![]() ,即可求证;
,即可求证;
(2)由题以![]() 为原点,
为原点,![]() 为坐标轴建立空间坐标系
为坐标轴建立空间坐标系![]() ,设
,设![]() ,
,![]() ,分别求得平面
,分别求得平面![]() 与平面
与平面![]() 的法向量,进而利用数量积求解即可.
的法向量,进而利用数量积求解即可.
(1)证明:连接![]() ,
,![]() ,
,

由题,因为![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
又![]() ,所以四边形
,所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,即
,即![]() ,
,
所以![]() ,且
,且![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)解:存在,
以![]() 为原点,
为原点,![]() 为坐标轴建立如图所示的坐标系
为坐标轴建立如图所示的坐标系![]() ,如图所示,
,如图所示,
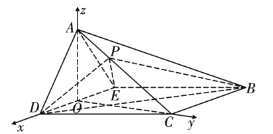
不妨设棱长![]() ,由(1)可知
,由(1)可知![]() 是等边三角形,
是等边三角形,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,且
,且![]() ,
,![]() ,
,
则![]() ,
,
可得![]() ,则
,则![]() ,
,![]() ,
,
设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
则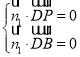 ,即
,即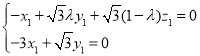 ,
,
令![]() ,则
,则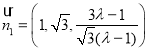 ,
,
由(1)知![]() 平面
平面![]() ,则
,则![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
若存在点![]() ,使平面
,使平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,
,
则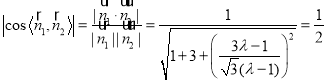 ,
,
解得![]() ,
,
所以存在点![]() ,使平面
,使平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,此时
,此时![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数组![]() ,如果数组
,如果数组![]() 满足
满足![]() ,且
,且![]() ,其中
,其中![]()
![]() ,则称
,则称![]() 为
为![]() 的“兄弟数组”.
的“兄弟数组”.
(1)写出数组![]() 的“兄弟数组”
的“兄弟数组”![]() ;
;
(2)若![]() 的“兄弟数组”是
的“兄弟数组”是![]() ,试证明:
,试证明:![]() 成等差数列;
成等差数列;
(3)若![]() 为偶数,且
为偶数,且![]() 的“兄弟数组”是
的“兄弟数组”是![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax+1(a∈R).
(1)求f(x)的单调区间;
(2)设g(x)=lnx![]() ,若对任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,求实数a的取值范围.
,若对任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高三年级不同性别的学生对体育课改上自习课的态度(肯定还是否定),进行了如下的调查研究.全年级共有![]() 名学生,男女生人数之比为
名学生,男女生人数之比为![]() ,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为
,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为![]() .
.
(1)求抽取的男学生人数和女学生人数;
(2)通过对被抽取的学生的问卷调查,得到如下![]() 列联表:
列联表:
否定 | 肯定 | 总计 | |
男生 | 10 | ||
女生 | 30 | ||
总计 |
①完成列联表;
②能否有![]() 的把握认为态度与性别有关?
的把握认为态度与性别有关?
(3)若一班有![]() 名男生被抽到,其中
名男生被抽到,其中![]() 人持否定态度,
人持否定态度,![]() 人持肯定态度;二班有
人持肯定态度;二班有![]() 名女生被抽到,其中
名女生被抽到,其中![]() 人持否定态度,
人持否定态度,![]() 人持肯定态度.
人持肯定态度.
现从这![]() 人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.
人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.
解答时可参考下面临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明.下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用![]() ,化简,得
,化简,得![]() .设勾股形中勾股比为
.设勾股形中勾股比为![]() ,若向弦图内随机抛掷
,若向弦图内随机抛掷![]() 颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为![]() (
(![]() 为参数),在以O为极点,x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为
为参数),在以O为极点,x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为![]()
(1)求曲线C的直角坐标方程
(2)设直线l与x轴交于点P,且与曲线C相交与A、B两点,若![]() 是
是![]() 与
与![]() 的等比中项,求实数m的值
的等比中项,求实数m的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为服用同等剂量的三种新药后血药浓度![]() 的变化情况,其中点
的变化情况,其中点![]() 的横坐标表示服用第
的横坐标表示服用第![]() 种药后血药浓度达峰(最高浓度)时间,其它点的横坐标分别表示服用三种新药后血药浓度首次降到峰值一半时所用的时间(单位:
种药后血药浓度达峰(最高浓度)时间,其它点的横坐标分别表示服用三种新药后血药浓度首次降到峰值一半时所用的时间(单位:![]() ),点
),点![]() 的纵坐标表示第
的纵坐标表示第![]() 种药的血药浓度的峰值
种药的血药浓度的峰值![]() . 记
. 记![]() 为服用第
为服用第![]() 种药后达到血药浓度峰值时,血药浓度提高的平均速度,记
种药后达到血药浓度峰值时,血药浓度提高的平均速度,记![]() 为服用第
为服用第![]() 种药后血药浓度从峰值首次降到峰值的一半所用的时间,则
种药后血药浓度从峰值首次降到峰值的一半所用的时间,则![]() 中最小的,
中最小的,![]() 中最大的分别是( )
中最大的分别是( )
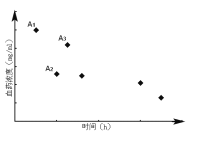
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为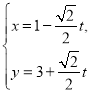 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程及
的普通方程及![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求
上,求![]() 的最小值及此时点
的最小值及此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com