
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为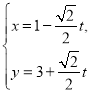 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程及
的普通方程及![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求
上,求![]() 的最小值及此时点
的最小值及此时点![]() 的直角坐标.
的直角坐标.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
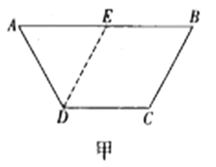
【题目】如图甲,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使二面角
折起,使二面角![]() 为
为![]() ,连接
,连接![]() ,
,![]() 得到四棱锥
得到四棱锥![]() (如图乙),
(如图乙),![]() 为
为![]() 的中点,
的中点,![]() 是棱
是棱![]() 上一点.
上一点.
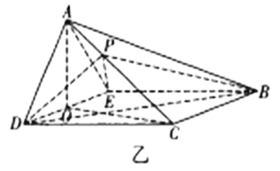
(1)求证:当![]() 为
为![]() 的中点时,平面
的中点时,平面![]() 平面
平面![]() ;
;
(2)是否存在一点![]() ,使平面
,使平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,若存在,求
,若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,圆C的参数方程为![]() (θ为参数),直线l经过定点P(2,3),倾斜角为
(θ为参数),直线l经过定点P(2,3),倾斜角为![]() .
.
(Ⅰ)写出直线l的参数方程和圆C的标准方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA|·|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图①中△ABC 为直角三角形![]() D、E 分别为 AB、AC 的中点,将△ADE 沿 DE 折起使平面 ADE⊥BCED,连接 AB,AC,BE如图②所示.
D、E 分别为 AB、AC 的中点,将△ADE 沿 DE 折起使平面 ADE⊥BCED,连接 AB,AC,BE如图②所示.
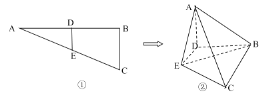
(1)在线段AC上找一点P,使EP∥平面ABD,并求出异面直线AB、EP所成的角;
(2)在平面ABD内找一点Q,使PQ⊥平面ABE,并求三棱锥P-ABE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
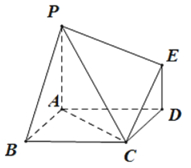
【题目】如图,已知多面体![]() 的底面
的底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() 平面
平面![]() ,
,![]() ,且
,且![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为45°,求平面
所成的角为45°,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,令
时,令![]() ,是否存在区间
,是否存在区间![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,若存在,求实数
,若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凤梨穗龙眼原产厦门,是厦门市的名果,栽培历史已有100多年.龙眼干的级别按直径![]() 的大小分为四个等级(如下表).
的大小分为四个等级(如下表).
|
|
|
|
|
级别 | 三级品 | 二级品 | 一级品 | 特级品 |
某商家为了解某农场一批龙眼干的质量情况,随机抽取了100个龙眼干作为样本(直径分布在区间![]() ),统计得到这些龙眼干的直径的频数分布表如下:
),统计得到这些龙眼干的直径的频数分布表如下:
|
|
|
|
|
|
频数 | 1 |
| 29 |
| 7 |
用分层抽样的方法从样本的一级品和特级品中抽取6个,其中一级品有2个.
(1)求![]() 、
、![]() 的值,并估计这批龙眼干中特级品的比例;
的值,并估计这批龙眼干中特级品的比例;
(2)已知样本中的100个龙眼干约500克,该农场有500千克龙眼干待出售,商家提出两种收购方案:
方案![]() :以60元/千克收购;
:以60元/千克收购;
方案![]() :以级别分装收购,每袋100个,特级品40元/袋、一级品30元/袋、二级品20元/袋、三级品10元/袋.
:以级别分装收购,每袋100个,特级品40元/袋、一级品30元/袋、二级品20元/袋、三级品10元/袋.
用样本的频率分布估计总体分布,哪个方案农场的收益更高?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com