[题目]已知在直角坐标系xOy中.圆C的参数方程为 (θ为参数).直线l经过定点P(2.3).倾斜角为.(Ⅰ)写出直线l的参数方程和圆C的标准方程,(Ⅱ)设直线l与圆C相交于A.B两点.求|PA|·|PB|的值. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知在直角坐标系xOy中，圆C的参数方程为 (θ为参数)，直线l经过定点P(2，3)，倾斜角为.

(Ⅰ)写出直线l的参数方程和圆C的标准方程；

(Ⅱ)设直线l与圆C相交于A，B两点，求｜PA｜·｜PB｜的值.

【答案】(Ⅰ) 圆C方程为：，直线的参数方程为 (t为参数)；(Ⅱ)3.

【解析】试题分析：

(Ⅰ)利用题中所给的方程可得圆C方程为：，直线的参数方程为 (t为参数)；

(Ⅱ)联立直线的参数方程与圆的普通方程，结合韦达定理可得｜PA｜·｜PB｜的值是3.

试题解析：

(Ⅰ)圆C方程为： ①，直线的参数方程为 (t为参数)②

(Ⅱ)把②代人①得， ③,设t1,t2是方程③的两个实根，则t1t2=-3,所以｜PA｜·｜PB｜=|t1t2|=3

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某校随机调查了80位学生，以研究学生中爱好羽毛球运动与性别的关系，得到下面的列联表：

	爱好	不爱好	合计
男	20	30	50
女	10	20	30
合计	30	50	80

（Ⅰ）将此样本的频率估计为总体的概率，随机调查了本校的3名学生，设这3人中爱好羽毛球运动的人数为，求的分布列，数学期望及方差；

（Ⅱ）根据表中数据，能否有充分证据判断爱好羽毛球运动与性别有关？若有，有多大把握？

	0.500	0.100	0.050	0.010
	0.455	2.706	3.841	6.635

附：

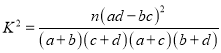
查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知数列的前n项和，是等差数列，且.

（Ⅰ）求数列的通项公式；

（Ⅱ）令.求数列的前n项和.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在几何体中，四边形是菱形，平面, , .

（1）证明：平面平面.

（2）若二面角是直二面角，求与平面所成角的正切值。

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图所示，圆锥的轴截面为等腰直角△SAB，Q为底面圆周上一点.

(1)若QB的中点为C，OH⊥SC，求证：OH⊥平面SBQ；

(2)如果∠AOQ＝60°，QB＝2，求此圆锥的体积.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】信息科技的进步和互联网商业模式的兴起，全方位地改变了大家金融消费的习惯和金融交易模式，现在银行的大部分业务都可以通过智能终端设备完成，多家银行职员人数在悄然减少.某银行现有职员320人，平均每人每年可创利20万元.据评估，在经营条件不变的前提下，每裁员1人，则留岗职员每人每年多创利0.2万元，但银行需付下岗职员每人每年6万元的生活费，并且该银行正常运转所需人数不得小于现有职员的，为使裁员后获得的经济效益最大，该银行应裁员多少人？此时银行所获得的最大经济效益是多少万元？