
【题目】函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,方程
时,方程![]() 在区间
在区间![]() 内有唯一实数解,求实数
内有唯一实数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)答案见解析;(2) ![]() 或
或![]() .
.
【解析】试题分析:
(1)求导,分类讨论得f(x)的单调区间即可;
(2)问题转化为![]() 有唯一实数解;构造函数,求导得
有唯一实数解;构造函数,求导得![]() 或
或![]() .
.
试题解析:
(1) ![]() ,
,
(i)当![]() 时,
时, ![]() ,令
,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
函数f(x)在![]() 上单调递增,
上单调递增, ![]() 上单调递减;
上单调递减;
(ⅱ)当![]() 时,令
时,令![]() ,得
,得![]()
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
函数f(x)在![]() 和
和![]() 上单调递增,
上单调递增, ![]() 上单调递减;
上单调递减;
(ⅲ)当![]() 时,
时, ![]() ,函数f(x)在
,函数f(x)在![]() 上单调递增;
上单调递增;
(ⅳ)当![]() 时,
时, ![]()
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
函数f(x)在![]() 和
和![]() 上单调递增,
上单调递增, ![]() 上单调递减;
上单调递减;
综上所述:当![]() 时,函数f(x)的单调递增区间为
时,函数f(x)的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,函数f(x)的单调递增区间为
时,函数f(x)的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,函数f(x)的单调递增区间为
时,函数f(x)的单调递增区间为![]() ;
;
当![]() 时,函数f(x)的单调递增区间为
时,函数f(x)的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]()
(2)当![]() 时,
时, ![]() ,由
,由![]() ,得
,得![]() ,又
,又![]() ,所以
,所以![]() ,
,
要使方程![]() 在区间
在区间![]() 上有唯一实数解,只需
上有唯一实数解,只需![]() 有唯一实数解;
有唯一实数解;
令![]() ,∴
,∴![]() ,
,
由![]() 得
得![]() 得
得![]() ,
,
∴![]() 在区间
在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上是减函数.
上是减函数.
![]() ,
,
故![]() 或
或![]()


科目:高中数学 来源: 题型:
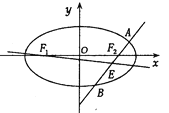
【题目】已知椭圆![]() 的方程为
的方程为![]() ,双曲线
,双曲线![]() 的一条渐近线与
的一条渐近线与![]() 轴所成的夹角为
轴所成的夹角为![]() ,且双曲线的焦距为
,且双曲线的焦距为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 分别为椭圆
分别为椭圆![]() 的左,右焦点,过
的左,右焦点,过![]() 作直线
作直线![]() (与
(与![]() 轴不重合)交椭圆于
轴不重合)交椭圆于![]() ,
, ![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
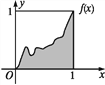
【题目】设函数y=f(x)在区间[0,1]上的图象是连续不断的一条曲线,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算由曲线y=f(x)及直线x=0,x=1,y=0所围成部分的面积S.先产生两组(每组N个)0~1区间上的均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N).再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方法可得S的近似值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,圆C的参数方程为![]() (θ为参数),直线l经过定点P(2,3),倾斜角为
(θ为参数),直线l经过定点P(2,3),倾斜角为![]() .
.
(Ⅰ)写出直线l的参数方程和圆C的标准方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA|·|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲,乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
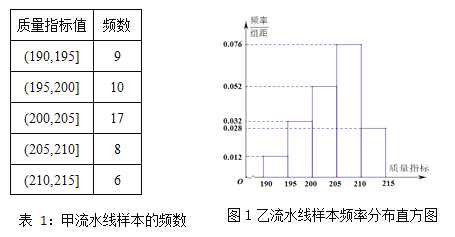
(1)根据图,1估计乙流水线生产产品该质量指标值的中位数;
(2)若将频率视为概率,某个月内甲,乙两条流水线均生产了5000件产品,则甲,乙两条流水线分别生产出不合格品约多少件?
(3)根据已知条件完成下面![]() 列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
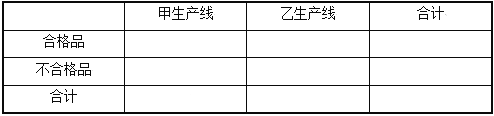
附: ![]() (其中
(其中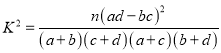 为样本容量)
为样本容量)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.已知曲线
轴的正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .倾斜角为
.倾斜角为![]() ,且经过定点
,且经过定点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)写出直线![]() 的参数方程的标准形式,并求曲线
的参数方程的标准形式,并求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场有奖销售中,购满100元商品得1张奖券,多购多得.1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C,求:
(1)P(A),P(B),P(C).
(2)1张奖券的中奖概率.
(3)1张奖券不中特等奖,且不中一等奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com