
【题目】图①中△ABC 为直角三角形![]() D、E 分别为 AB、AC 的中点,将△ADE 沿 DE 折起使平面 ADE⊥BCED,连接 AB,AC,BE如图②所示.
D、E 分别为 AB、AC 的中点,将△ADE 沿 DE 折起使平面 ADE⊥BCED,连接 AB,AC,BE如图②所示.
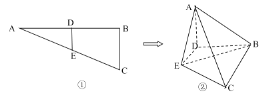
(1)在线段AC上找一点P,使EP∥平面ABD,并求出异面直线AB、EP所成的角;
(2)在平面ABD内找一点Q,使PQ⊥平面ABE,并求三棱锥P-ABE的体积.
【答案】(1)点P为AC的中点,![]() (2)Q为DF的中点,
(2)Q为DF的中点,![]()
【解析】
(1)分别取 AC、AB 的中点 P、F,依次连 EP、PF、FD,先证四边形![]() 为平行四边形,再利用线面平行的判定即可得解;由等腰三角形的性质可得
为平行四边形,再利用线面平行的判定即可得解;由等腰三角形的性质可得![]() ,即可得
,即可得![]() ,即可得解;
,即可得解;
(2)过P作![]() 并延长DF于Q,先证明
并延长DF于Q,先证明![]() 平面ABE,再通过平面几何知识求证
平面ABE,再通过平面几何知识求证![]() 即可得解;求出
即可得解;求出![]() 和PO长度即可求得体积.
和PO长度即可求得体积.
(1)分别取 AC、AB 的中点 P、F,依次连 EP、PF、FD,
则![]() 且
且![]() ,
,
![]() D、E 分别为 AB、AC 的中点,
D、E 分别为 AB、AC 的中点,
![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]() 即四边形
即四边形![]() 为平行四边形,
为平行四边形,
![]()
![]()
又![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,
即所求的点P为AC的中点,
![]()
![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,![]()
![]() ,
,
故异面直线 AB、EP 所成的夹角为![]()
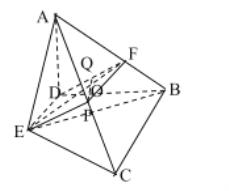
(2)连结EF,因为![]() ,
,![]() ,
,![]()
![]() 平面ABD,
平面ABD,
![]() 平面ABD,
平面ABD,![]()
![]() ,
,
又![]() ,
,![]() ,
,![]()
![]() 平面DEPF,
平面DEPF,
又![]() 平面ABE,
平面ABE,
![]() 平面
平面![]() 平面DEPF,且平面
平面DEPF,且平面![]() 平面
平面![]() ,
,
在平面DEPF中,过P作![]() 并延长DF于Q,则
并延长DF于Q,则![]() 平面ABE,
平面ABE,
因为四边形DEPF是矩形,且PF=DE=1,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
知Q为DF的中点,
在![]() 中,
中, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax+1(a∈R).
(1)求f(x)的单调区间;
(2)设g(x)=lnx![]() ,若对任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,求实数a的取值范围.
,若对任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
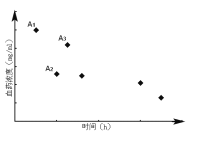
【题目】如图为服用同等剂量的三种新药后血药浓度![]() 的变化情况,其中点
的变化情况,其中点![]() 的横坐标表示服用第
的横坐标表示服用第![]() 种药后血药浓度达峰(最高浓度)时间,其它点的横坐标分别表示服用三种新药后血药浓度首次降到峰值一半时所用的时间(单位:
种药后血药浓度达峰(最高浓度)时间,其它点的横坐标分别表示服用三种新药后血药浓度首次降到峰值一半时所用的时间(单位:![]() ),点
),点![]() 的纵坐标表示第
的纵坐标表示第![]() 种药的血药浓度的峰值
种药的血药浓度的峰值![]() . 记
. 记![]() 为服用第
为服用第![]() 种药后达到血药浓度峰值时,血药浓度提高的平均速度,记
种药后达到血药浓度峰值时,血药浓度提高的平均速度,记![]() 为服用第
为服用第![]() 种药后血药浓度从峰值首次降到峰值的一半所用的时间,则
种药后血药浓度从峰值首次降到峰值的一半所用的时间,则![]() 中最小的,
中最小的,![]() 中最大的分别是( )
中最大的分别是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)当a=0时,求函数f (x)的单调减区间;
(2)已知函数f (x)的导函数f (x)有三个零点x1,x2,x3(x1 x2 x3).①求a的取值范围;②若m1,m2(m1 m2)是函数f (x)的两个零点,证明:x1m1x1 1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为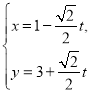 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程及
的普通方程及![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求
上,求![]() 的最小值及此时点
的最小值及此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行运动会,其中三级跳远的成绩在![]() 米以上的进入决赛,把所得的数据进行整理后,分成
米以上的进入决赛,把所得的数据进行整理后,分成![]() 组画出频率分布直方图的一部分(如图),已知第
组画出频率分布直方图的一部分(如图),已知第![]() 组的频数是
组的频数是![]() .
.
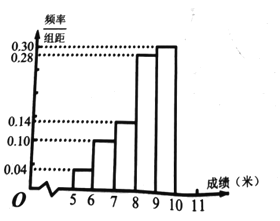
(1)求进入决赛的人数;
(2)经过多次测试后发现,甲的成绩均匀分布在![]() 米之间,乙的成绩均匀分布在
米之间,乙的成绩均匀分布在![]() 米之间,现甲、乙各跳一次,求甲比乙远的概率.
米之间,现甲、乙各跳一次,求甲比乙远的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com