练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （06年浙江卷理）（14分）

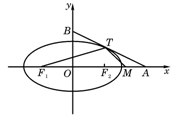
    如图，椭圆＝1（a＞b＞0）与过点A（2，0）B(0,1)的直线有且只有一个公共点T，且椭圆的离心率e=.

     (Ⅰ)求椭圆方程；

    (Ⅱ)设F、F分别为椭圆的左、右焦点，M为线段AF的中点，求证：∠ATM=∠AFT.

    本题主要考查直线与椭圆的位置关系、椭圆的几何性质，同时考察解析几何的基本思想方法和综合解题能力。

    解析：（I）过点、的直线方程为

    因为由题意得有惟一解，

    即有惟一解，

    所以

       （），

    故 

    又因为 即 

    所以 

    从而得 

    故所求的椭圆方程为   

    （II）由（I）得 

    故

    从而

    由

    解得

    所以

    因为

    又得

    因此

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

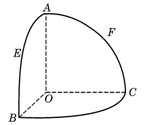
    （06年浙江卷理）如图，O是半径为l的球心，点A、B、C在球面上，OA、OB、OC两两垂直，E、F分别是大圆弧AB与AC的中点，则点E、F在该球面上的球面距离是

    (A)   　　　(B)    (C)         (D)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （06年浙江卷理）（14分）

    已知函数f(x)=x+ x，数列｜x｜(x＞0)的第一项x＝1，以后各项按如下方式取定：曲线x=f(x)在处的切线与经过（0，0）和（x,f (x)）两点的直线平行（如图）

    .

    求证：当n时，

      (Ⅰ)x 

    （Ⅱ）

     

    查看答案和解析>>

    同步练习册答案