
下表是关于某设备的使用年限(年)和所需要的维修费用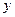 (万元)的几组统计数据:
(万元)的几组统计数据:
 | 2 | 3 | 4 | 5 | 6 |
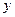 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
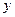 关于
关于 的线性回归方程
的线性回归方程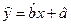 ;
;


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:解答题
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组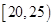 ,第2组
,第2组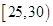 ,第3组
,第3组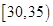 ,第4组
,第4组 ,第5组
,第5组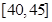 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.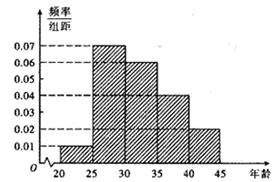
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高.然而也有部分公众对该活动的实际效果与负面影响提出了疑问.对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| | 支持 | 保留 | 不支持 |
| 20岁以下 | 800 | 450 | 200 |
| 20岁以上(含20岁) | 100 | 150 | 300 |
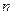 个人,已知从“支持”态度的人中抽取了45人,求
个人,已知从“支持”态度的人中抽取了45人,求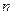 的值;
的值;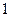 人20岁以下的概率;
人20岁以下的概率; 个数,求该数与总体平均数之差的绝对值超过0.6的概率.
个数,求该数与总体平均数之差的绝对值超过0.6的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂对某产品的产量与单位成本的资料分析后有如下数据:
| 月 份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 产量x千件 | 2 | 3 | 4 | 3 | 4 | 5 |
| 单位成本y元/件 | 73 | 72 | 71 | 73 | 69 | 68 |
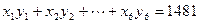 ,结果保留两位小数)
,结果保留两位小数)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量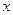 (吨)与相应的生产能耗
(吨)与相应的生产能耗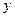 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
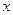 | 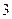 | 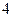 | 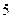 | 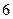 |
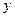 |  | 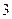 | 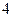 | 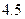 |
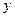 关于
关于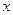 的线性回归方程
的线性回归方程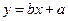 ;
; (参考数值:
(参考数值: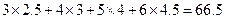 ,
,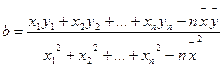 ,
,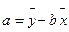 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种产品的广告费支出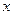 与销售额(单位:百万元)之间有如下对应数据:
与销售额(单位:百万元)之间有如下对应数据:
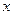 | 2 | 4 | 5 | 6 | 8 |
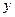 | 30 | 40 | 50 | 60 | 70 |
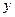 与
与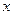 之间具有线性相关关系.
之间具有线性相关关系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克),重量的分组区间为(490,495],(495,500],……,(510,515],由此得到样本的频率分布直方图,如图4所示.根据频率分布直方图,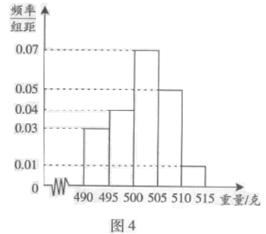
求(1)重量超过500 克的产品的频率;
(2)重量超过500 克的产品的数量.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)为了了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下: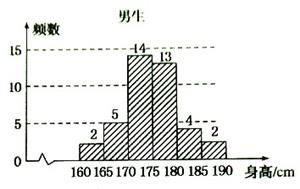
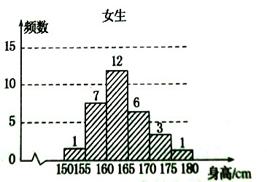
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3)从样本中身高在180~190cm之间的男生中任选2人,
求至少有1人身高在185~190cm之间的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了 50名学生.调査结果表明:在爱看课外书的25人中有18人作文水平好,另7人作文水平一般;在不爱看课外书的25人中有6人作文水平好,另19人作文水平一般.
(Ⅰ)试根据以上数据完成以下2×2列联表,并运用独 立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
高中学生的作文水平与爱看课外书的2×2列联表
| | 爱看课外书 | 不爱看课外书 | 总计 |
作文水平 好 好 | | | |
| 作文水平一般 | [来源:学。科。网Z。X。X。K] | | |
| 总计 | | | |
 分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.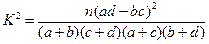 ,其中
,其中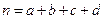 .
.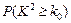 [来源:学*科*网] [来源:学*科*网] | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
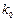 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com