
���� ���ݵ����ļ��������жϢ���ȷ�����ݵ����ͺ����ĵ������жϢڴ������ݵ��������㣬�õ�����ȷ�����ݵ����뺯���ĵ����ԵĹ�ϵ�жϢܴ������ݺ�����б�ʹ�ϵ����Ϻ����ĵ����Կ����жϢ���ȷ��
���  �⣺�٣���f�䣨x��=��x+1��ex���൱x=-1ʱ��f�䣨-1��=0������f��x������ƽ����x������ߣ��ʢ���ȷ��
�⣺�٣���f�䣨x��=��x+1��ex���൱x=-1ʱ��f�䣨-1��=0������f��x������ƽ����x������ߣ��ʢ���ȷ��
�ڣ���f�䣨x��=��x+1��ex����x�ʣ�-�ޣ�-1��ʱ������f��x�������ݼ���x�ʣ�-1��+�ޣ�ʱ������f��x������������
��$\frac{f��{x}_{1}��-f��{x}_{2}��}{{x}_{1}-{x}_{2}}$��0����ȷ�����ʢڴ���
�ۣ���f1��x��=f�䣨x0��=xex+2ex��f2��x��=f1�䣨x��=xex+3ex������fn��x��=f��n-1��x��=xex+��n+1��ex��
��f��2012��x��=f2013��x��=xex+2014ex���ʢ���ȷ��
�ܣ�f��x1��+x2��f��x2��+x1�ȼ���f��x1��-x1��f��x2��-x2����������h��x��=f��x��-x����h�䣨x��=f�䣨x��-1=��x+1��ex-1��
��֪����h��x����R�ϲ��������ʢܴ���
�ݣ���x1��0ʱ����x2f��x1����x1f��x2������ȼ�Ϊ$\frac{f��{x}_{1}��}{{x}_{1}}$��$\frac{f��{x}_{2}��}{{x}_{2}}$��
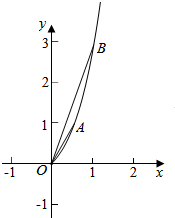
�������ڵ�A��x1��f��x1������B��x2��f��x2����������ԭ���б������kOA��kOB��
�ɢ�֪�����ڣ�0��+�ޣ��ϵ�����������kOA��kOB���������ʢ���ȷ��
�ʴ�Ϊ���٢ۢ�
���� ������Ҫ�����뵼���йص����������жϣ������˵����ļ��������Լ������ͺ����ĵ����ԵĹ�ϵ���Լ����������㷨�������е���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ��ƽ��PAB��ƽ��ABC��ƽ��PAC��ƽ��ABC��E�ǵ�A��ƽ��PBC�ڵ���Ӱ����֤��PA��ƽ��ABC��
��֪����ͼ��ƽ��PAB��ƽ��ABC��ƽ��PAC��ƽ��ABC��E�ǵ�A��ƽ��PBC�ڵ���Ӱ����֤��PA��ƽ��ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��$\frac{4}{3}$���ȣ�$\frac{4}{3}$��2�� | B�� | ��1��$\frac{4}{3}$���ȣ�$\frac{4}{3}$��+�ޣ� | C�� | ��1��2�� | D�� | ��1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com