
 sinxcosx+cos2x+a
sinxcosx+cos2x+a 时,函数f(x)的最大值与最小值的和为
时,函数f(x)的最大值与最小值的和为 ,解不等式f(x)>1.
,解不等式f(x)>1. sinxcosx+cos2x+a
sinxcosx+cos2x+a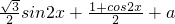
 )+a+
)+a+
 .
.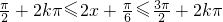 ,得
,得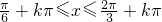 .
.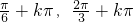 ](k∈Z).
](k∈Z).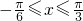 ,所以
,所以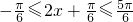 ,
,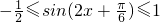 .
.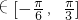 时,f(x)max+f(x)min=(1+a+
时,f(x)max+f(x)min=(1+a+ )+(-
)+(- +a+
+a+ )=
)= ,
, )+
)+ .
.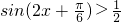
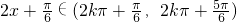
 .
. 时,先表示出f(x)的最值,再解得a,最后结合正弦函数的图象解得答案.
时,先表示出f(x)的最值,再解得a,最后结合正弦函数的图象解得答案.

科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 2 |
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| sinx+cosx-|sinx-cosx| |
| 2 |
| ||
| 2 |
| 5π |
| 3 |
| 17π |
| 6 |
| 5π |
| 3 |
| 17π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com