Question

已知M是正四面体ABCD棱AB的中点，N是棱CD的中点，则下列结论中，正确的个数有（ ）
（1）MN⊥AB；            
（2）V_A-MCD=V_B-MCD；     
（3）平面CDM⊥平面ABN； 
（4）CM与AN是相交直线．
A．1 个
B．2 个
C．3 个
D．4个

Answer 1

【答案】分析：连接CM、DM，可证明出AB⊥平面CDM，从而MN⊥AB，得（1）正确；根据（1）中结论可得棱锥A-MCD与棱锥B-MCD均又三角形MCD为底面，且高均为AB的一半，代入棱锥体积公式可得 V_A-MCD=V_B-MCD；，故（2）正确；根据（1）的正确结论：MN⊥AB，结合平面与平面垂直的判定定理，得到（3）正确；对于（4），可根据异面直线判定定理得到CM与AN异面．
解答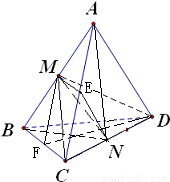：解：（1）连接CM、DM
∵正△ABC中，M为AB的中点
∴CM⊥AB
同理DM⊥AB，结合MC∩MD=M
∴AB⊥平面CDM，而MN⊆平面CDM
∴MN⊥AB，故（1）是正确的；
（2）棱锥A-MCD与棱锥B-MCD的底面均为三角形MCD，
由（1）得AB⊥平面CDM，
且M为AB的中点，
则棱锥A-MCD与棱锥B-MCD的高AM=BM
故V_A-MCD=V_B-MCD；
故（2）正确；
（3）由（1）的证明知：AB⊥平面CDM
∵AB?平面ABN
∴平面ABN⊥平面CDM，故（3）正确；
（4）CM∩平面ACD=C
AN?平面ACD且C∉AN．
故CM与AN是异面直线
综上所述，正确的命题为（1）（2）（3）
故选C
点评：本题以正四面体为例，着重考查了直线与平面垂直的判定、平面与平面垂直的判定和异面直线的判定等知识点，属于中档题．