
【题目】设![]() ,函数
,函数![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 内的极值;
内的极值;
(2)设函数![]() ,当
,当![]() 有两个极值点
有两个极值点![]() 时,总有
时,总有![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)极大值是![]() ,无极小值;(2)
,无极小值;(2)![]()
【解析】
(1)当![]() 时,可求得
时,可求得![]() ,令
,令![]() ,利用导数可判断
,利用导数可判断![]() 的单调性并得其零点,从而可得原函数的极值点及极大值;
的单调性并得其零点,从而可得原函数的极值点及极大值;
(2)表示出![]() ,并求得
,并求得![]() ,由题意,得方程
,由题意,得方程![]() 有两个不同的实根
有两个不同的实根![]() ,
,![]() ,从而可得△
,从而可得△![]() 及
及![]() ,由
,由![]() ,得
,得![]() .则
.则![]() 可化为
可化为![]() 对任意的
对任意的![]() 恒成立,按照
恒成立,按照![]() 、
、![]() 、
、![]() 三种情况分类讨论,分离参数
三种情况分类讨论,分离参数![]() 后转化为求函数的最值可解决;
后转化为求函数的最值可解决;
(1)当![]() 时,
时,![]() .
.
令![]() ,则
,则![]() ,显然
,显然![]() 在上
在上![]() 单调递减,
单调递减,
又因为![]() ,故
,故![]() 时,总有
时,总有![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
由于![]() ,所以当
,所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
| + | - | |
| 增 | 极大 | 减 |
所以![]() 在
在![]() 上的极大值是
上的极大值是![]() ,无极小值.
,无极小值.
(2)由于![]() ,则
,则![]() .由题意,方程
.由题意,方程![]() 有两个不等实根
有两个不等实根![]() ,则
,则![]() ,解得
,解得![]() ,且
,且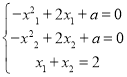 ,又
,又![]() ,所以
,所以![]() .
.
由![]() ,
,![]() ,可得
,可得![]()
又![]() .将其代入上式得:
.将其代入上式得:![]() .
.
整理得![]() ,即
,即![]()
当![]() 时,不等式
时,不等式![]() 恒成立,即
恒成立,即![]() .
.
当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() ,令
,令![]() ,易证
,易证![]() 是
是![]() 上的减函数.因此,当
上的减函数.因此,当![]() 时,
时,![]() ,故
,故![]() .
.
当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() ,
,
因此,当![]() 时,
时,![]() 所以
所以![]() .
.
综上所述,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的极坐标方程化为直角坐标方程,并说明曲线
的极坐标方程化为直角坐标方程,并说明曲线![]() 的形状;
的形状;
(2)若直线![]() 经过点
经过点![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 截得的线段的长.
截得的线段的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在古装电视剧《知否》中,甲乙两人进行一种投壶比赛,比赛投中得分情况分“有初”“贯耳”“散射”“双耳”“依竿”五种,其中“有初”算“两筹”,“贯耳”算“四筹”,“散射”算“五筹”,“双耳”算“六筹”,“依竿”算“十筹”,三场比赛得筹数最多者获胜.假设甲投中“有初”的概率为![]() ,投中“贯耳”的概率为
,投中“贯耳”的概率为![]() ,投中“散射”的概率为
,投中“散射”的概率为![]() ,投中“双耳”的概率为
,投中“双耳”的概率为![]() ,投中“依竿”的概率为
,投中“依竿”的概率为![]() ,乙的投掷水平与甲相同,且甲乙投掷相互独立.比赛第一场,两人平局;第二场,甲投了个“贯耳”,乙投了个“双耳”,则三场比赛结束时,甲获胜的概率为( )
,乙的投掷水平与甲相同,且甲乙投掷相互独立.比赛第一场,两人平局;第二场,甲投了个“贯耳”,乙投了个“双耳”,则三场比赛结束时,甲获胜的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图象关于直线
,其图象关于直线![]() 对称,为了得到函数
对称,为了得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象上的所有点( )
的图象上的所有点( )
A.先向左平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
B.先向右平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
C.先向右平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
D.先向左平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着“雾霾”天出现的越来越频繁,很多人为了自己的健康,外出时选择戴口罩,长郡中学高三兴趣研究小组利用暑假空闲期间做了一项对人们雾霾天外出时是否戴口罩的调查,共调查了120人,其中女性70人,男性50人,并根据统计数据画出等高条形图如图所示:
(Ⅰ)利用图形判断性别与雾霾天外出戴口罩是否有关系;
(Ⅱ)根据统计数据建立一个![]() 列联表;
列联表;
(Ⅲ)能否在犯错误的概率不超过0.05的前提下认为性别与雾霾天外出戴口罩有关系.
附: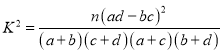

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 的各条棱长均相等,
的各条棱长均相等, ![]() 为
为![]() 的中点,
的中点, ![]() 分别是线段
分别是线段![]() 和线段
和线段![]() 上的动点(含端点),且满足
上的动点(含端点),且满足![]() .当
.当![]() 运动时,下列结论中不正确的是( )
运动时,下列结论中不正确的是( )
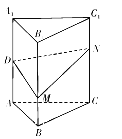
A. 平面![]() 平面
平面![]() B. 三棱锥
B. 三棱锥![]() 的体积为定值
的体积为定值
C. ![]() 可能为直角三角形 D. 平面
可能为直角三角形 D. 平面![]() 与平面
与平面![]() 所成的锐二面角范围为
所成的锐二面角范围为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】扇形AOB中心角为![]() ,所在圆半径为
,所在圆半径为![]() ,它按如图(Ⅰ)(Ⅱ)两种方式有内接矩形CDEF.
,它按如图(Ⅰ)(Ⅱ)两种方式有内接矩形CDEF.

(1)矩形CDEF的顶点C、D在扇形的半径OB上,顶点E在圆弧AB上,顶点F在半径OA上,设![]() ;
;
(2)点M是圆弧AB的中点,矩形CDEF的顶点D、E在圆弧AB上,且关于直线OM对称,顶点C、F分别在半径OB、OA上,设![]() ;
;
试研究(1)(2)两种方式下矩形面积的最大值,并说明两种方式下哪一种矩形面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:①函数![]() ;
;
②向量![]() ,
,![]() ,且
,且![]() ,
,![]() ;
;
③函数![]() 的图象经过点
的图象经过点![]()
请在上述三个条件中任选一个,补充在下面问题中,并解答.
已知_________________,且函数![]() 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)求函数![]() 在
在![]() 上的单调递减区间.
上的单调递减区间.
注:如果选择多个条件分别解答,按第一个解答计分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 是线段
是线段![]() 的中点,直线
的中点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com