已知数列{an}中,a1=1,a2=3,且an+1=an+2an-1(n≥2).
(1)设bn=an+1+λan,是否存在实数λ,使数列{bn}为等比数列.若存在,求出λ的值,若不存在,请说明理由;
(2)求数列{an}的前n项和Sn.
(本小题满分14分)
(1)方法1:假设存在实数λ,使数列{b
n}为等比数列,
则有
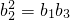
. ①…(1分)
由a
1=1,a
2=3,且a
n+1=a
n+2a
n-1,得a
3=5,a
4=11.
所以b
1=a
2+λa
1=3+λ,b
2=a
3+λa
2=5+3λ,b
3=a
4+λa
3=11+5λ,…(2分)
所以(5+3λ)
2=(3+λ)(11+5λ),
解得λ=1或λ=-2.…(3分)
当λ=1时,b
n=a
n+1+a
n,b
n-1=a
n+a
n-1,且b
1=a
2+a
1=4,
有
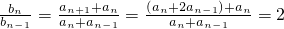
(n≥2).…(4分)
当λ=-2时,b
n=a
n+1-2a
n,b
n-1=a
n-2a
n-1,且b
1=a
2-2a
1=1,
有
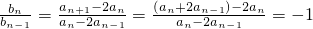
(n≥2).…(5分)
所以存在实数λ,使数列{b
n}为等比数列.
当λ=1时,数列{b
n}为首项是4、公比是2的等比数列;
当λ=-2时,数列{b
n}为首项是1、公比是-1的等比数列.…(6分)
方法2:假设存在实数λ,使数列{b
n}为等比数列,
设

(n≥2),…(1分)
即a
n+1+λa
n=q(a
n+λa
n-1),…(2分)
即a
n+1=(q-λ)a
n+qλa
n-1.…(3分)
与已知a
n+1=a
n+2a
n-1比较,令
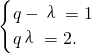
…(4分)
解得λ=1或λ=-2.…(5分)
所以存在实数λ,使数列{b
n}为等比数列.
当λ=1时,数列{b
n}为首项是4、公比是2的等比数列;
当λ=-2时,数列{b
n}为首项是1、公比是-1的等比数列.…(6分)
(2)解法1:由(1)知
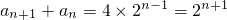
(n≥1),…(7分)
当n为偶数时,S
n=(a
1+a
2)+(a
3+a
4)+(a
5+a
6)+…+(a
n-1+a
n)…(8分)
=2
2+2
4+2
6+…+2
n…(9分)
=
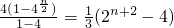
.…(10分)
当n为奇数时,S
n=a
1+(a
2+a
3)+(a
4+a
5)+…+(a
n-1+a
n)…(11分)
=1+2
3+2
5+…+2
n…(12分)
=
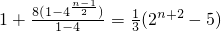
.…(13分)
故数列{a
n}的前n项和
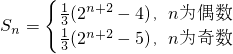
…(14分)
注:若将上述和式合并,即得
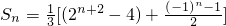
.
解法2:由(1)知
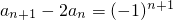
(n≥1),…(7分)
所以
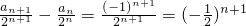
(n≥1),…(8分)
当n≥2时,
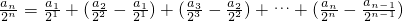
=
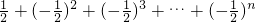
=
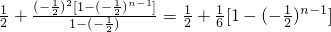
.
因为
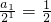
也适合上式,…(10分)
所以

=

(n≥1).
所以
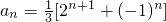
.…(11分)
则
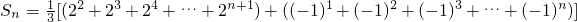
,…(12分)
=
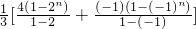
…(13分)
=
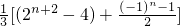
.…(14分)
解法3:由(1)可知,
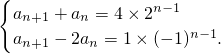
…(7分)
所以
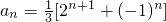
.…(8分)
则
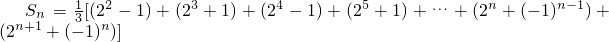
,…(9分)
当n为偶数时,
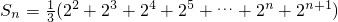
…(10分)
=
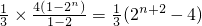
.…(11分)
当n为奇数时,
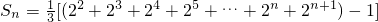
…(12分)
=
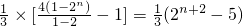
.…(13分)
故数列{a
n}的前n项和
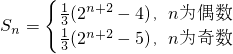
…(14分)
注:若将上述和式合并,即得
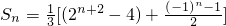
.
分析:(1)方法1:假设存在实数λ,使数列{b
n}为等比数列,通过
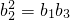
以及a
n+1=a
n+2a
n-1,解得λ=1或λ=-2,λ=1,λ=-2,分别说明数列{b
n}为等比数列.
方法2:假设存在实数λ,使数列{b
n}为等比数列,设

(n≥2),转化为a
n+1+λa
n=q(a
n+λa
n-1),就是a
n+1=(q-λ)a
n+qλa
n-1,与a
n+1=a
n+2a
n-1比较,
解得λ=1或λ=-2,存在实数λ,使数列{b
n}为等比数列.
(2)解法1:由(1)知
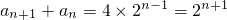
(n≥1),当n为偶数时,当n为奇数时,分别求出数列{a
n}的前n项和.
解法2:由(1)知
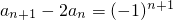
(n≥1),构造
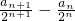
(n≥1),通过拆项法求出{

}的通项公式,然后求出数列的前n项和.
解法3:由(1)可知,
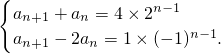
,求出
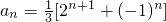
,当n为偶数时,
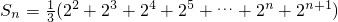
;当n为奇数时,
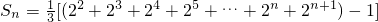
,分别求出数列{a
n}的前n项和.
点评:本题考查数列的递推关系式的应用,数列的通项公式的求法,前n项和的求法,拆项法,构造法的应用,考查分析问题解决问题的能力,计算能力,难度比较大.

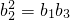 . ①…(1分)
. ①…(1分)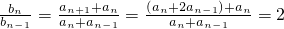 (n≥2).…(4分)
(n≥2).…(4分)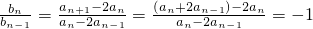 (n≥2).…(5分)
(n≥2).…(5分) (n≥2),…(1分)
(n≥2),…(1分)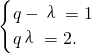 …(4分)
…(4分)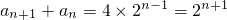 (n≥1),…(7分)
(n≥1),…(7分)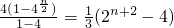 .…(10分)
.…(10分)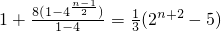 .…(13分)
.…(13分)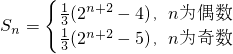 …(14分)
…(14分)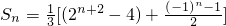 .
.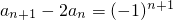 (n≥1),…(7分)
(n≥1),…(7分)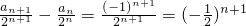 (n≥1),…(8分)
(n≥1),…(8分)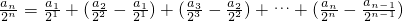
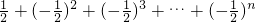
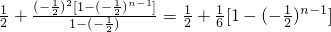 .
.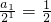 也适合上式,…(10分)
也适合上式,…(10分) =
= (n≥1).
(n≥1).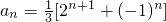 .…(11分)
.…(11分)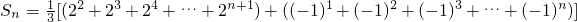 ,…(12分)
,…(12分)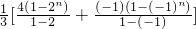 …(13分)
…(13分)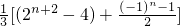 .…(14分)
.…(14分)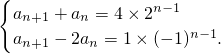 …(7分)
…(7分)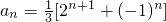 .…(8分)
.…(8分)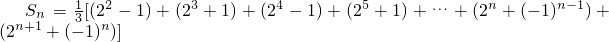 ,…(9分)
,…(9分)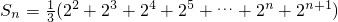 …(10分)
…(10分)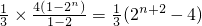 .…(11分)
.…(11分)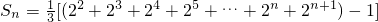 …(12分)
…(12分)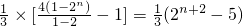 .…(13分)
.…(13分)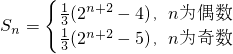 …(14分)
…(14分)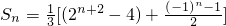 .
.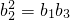 以及an+1=an+2an-1,解得λ=1或λ=-2,λ=1,λ=-2,分别说明数列{bn}为等比数列.
以及an+1=an+2an-1,解得λ=1或λ=-2,λ=1,λ=-2,分别说明数列{bn}为等比数列. (n≥2),转化为an+1+λan=q(an+λan-1),就是an+1=(q-λ)an+qλan-1,与an+1=an+2an-1比较,
(n≥2),转化为an+1+λan=q(an+λan-1),就是an+1=(q-λ)an+qλan-1,与an+1=an+2an-1比较,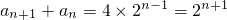 (n≥1),当n为偶数时,当n为奇数时,分别求出数列{an}的前n项和.
(n≥1),当n为偶数时,当n为奇数时,分别求出数列{an}的前n项和.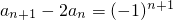 (n≥1),构造
(n≥1),构造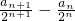 (n≥1),通过拆项法求出{
(n≥1),通过拆项法求出{ }的通项公式,然后求出数列的前n项和.
}的通项公式,然后求出数列的前n项和.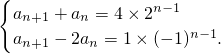 ,求出
,求出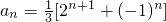 ,当n为偶数时,
,当n为偶数时,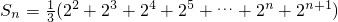 ;当n为奇数时,
;当n为奇数时,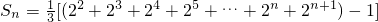 ,分别求出数列{an}的前n项和.
,分别求出数列{an}的前n项和.
