
| 7 |
| 10 |
| 7 |
| 10 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
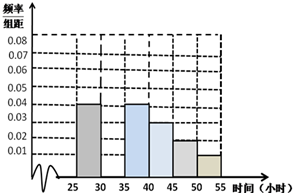 教育部,体育总局和共青团中央号召全国各级各类学校要广泛,深入地开展全国亿万大,中学生阳光体育运动,为此,某校学生会对高二年级2014年9月与10月这两个月内参加体育运动的情况进行统计,随机抽取了100名学生作为样本,得到这100名学生在该月参加体育运动总时间的小时数,根据此数据作出了如下的频数和频率的统计表和 频率分布直方图:
教育部,体育总局和共青团中央号召全国各级各类学校要广泛,深入地开展全国亿万大,中学生阳光体育运动,为此,某校学生会对高二年级2014年9月与10月这两个月内参加体育运动的情况进行统计,随机抽取了100名学生作为样本,得到这100名学生在该月参加体育运动总时间的小时数,根据此数据作出了如下的频数和频率的统计表和 频率分布直方图:| 分组 | 运动时间 (小时) | 频数 | 频率 |
| 1 | [25,30) | 20 | 0.2 |
| 2 | [30,35) | a | p |
| 3 | [35,40) | 20 | 0.2 |
| 4 | [40,45) | 15 | 0.15 |
| 5 | [45,50) | 10 | 0.10 |
| 6 | [50,55] | 5 | 0.05 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com