
判断函数f(x)=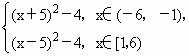 的奇偶性.
的奇偶性.
|
|
|
分析:本题若画出图象,可直现形象地看出其奇偶性,但是不严格;利用定义判断此函数的奇偶性,需分x∈(-6,-1],x∈[1,6)两种情况说明. 评注:(1)分段函数的奇偶性应分段证明f(-x)与f(x)的关系,只有当对称的两段上都满足相同的关系时才能判断其奇偶性. (2)若证明当x∈(-6,-l],f(-x)与f(x)的关系时,x∈(-6,-l],则-x∈[1,6),其中的f(-x)应将-x代入[1,6)的表达式中,得到的(x+5)2-4=f(x)正好是x∈(-6,-l]的表达式,若x∈[1,6)时,同理. (3)若f(x)是定义在R上的奇函数时,必有f(0)=0. |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com