
 成立的概率是
成立的概率是 ;
; ).
). 相对应的区域是以原点为圆心,半径为
相对应的区域是以原点为圆心,半径为 的圆在第一象限内的扇形,
的圆在第一象限内的扇形, 成立的概率等于
成立的概率等于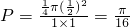 ,故③错误;
,故③错误; )上是减函数,
)上是减函数, ,+∞)上是增函数,
,+∞)上是增函数, )=1-
)=1- a2>0,可得a∈Φ;
a2>0,可得a∈Φ;  ),
), ),故④正确.
),故④正确. 

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| y-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 12 |
| π |
| 12 |
| x |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2x-1 |
| (1+2x)2 |
| x•2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com