
分析 先求出直线RQ的斜率kRQ=$\sqrt{3}-2$,再求出直线RQ的方程,从而求出Q点坐标,利用入射光线PQ和反射光线QR的性质,利用夹角公式求出PQ的斜率,进而求出PQ的直线方程,从而得到P点坐标,由此能求出△PQR的周长和面积.
解答 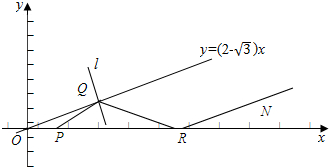 解:如图,由题意得直线PQ被直线l:y=(2-$\sqrt{3}$)x反射到达点R(10+10$\sqrt{3}$,0)后又被x轴反射,得到直线RN,
解:如图,由题意得直线PQ被直线l:y=(2-$\sqrt{3}$)x反射到达点R(10+10$\sqrt{3}$,0)后又被x轴反射,得到直线RN,
且RN∥l,
∴直线RN的斜率${k}_{RN}=2-\sqrt{3}$,∴直线RQ的斜率kRQ=$\sqrt{3}-2$,法线l′的斜率k′=-$\frac{1}{{k}_{RN}}$=-$\frac{1}{2-\sqrt{3}}$=-2-$\sqrt{3}$,
∴直线RQ的方程为:$y=(\sqrt{3}-2)[x-(10+10\sqrt{3})]$,
解方程组$\left\{\begin{array}{l}{y=(2-\sqrt{3})x}\\{y=(\sqrt{3}-2)[x-(10+10\sqrt{3})]}\end{array}\right.$,得Q(5$\sqrt{3}$+5,5$\sqrt{3}$-5),
设直线PQ的斜率为k,l′是入射光线PQ和反射光线QR的法线,
∴|$\frac{k-(-2-\sqrt{3})}{1+(-2-\sqrt{3})k}$|=|$\frac{(\sqrt{3}-2)-(-2-\sqrt{3})}{1+(\sqrt{3}-2)(-2-\sqrt{3})}$|,
解得k=1,或k=-$\frac{1}{2\sqrt{3}+2}$(舍),
∴直线PQ的方程为y-(5$\sqrt{3}$-5)=x-(5$\sqrt{3}$+5),
令y=0,得P(10,0),
∴|PQ|=$\sqrt{(5\sqrt{3}+5-10)^{2}+(5\sqrt{3}-5-0)^{2}}$=($5\sqrt{3}-5$)$\sqrt{2}$,
|QR|=$\sqrt{(5\sqrt{3}+5-10-10\sqrt{3})^{2}+(5\sqrt{3}-5-0)^{2}}$=10$\sqrt{2}$,
|PR|=(10+10$\sqrt{3}$)-10=10$\sqrt{3}$,
∴△PQR的周长为L=|PQ|+|PR|+|QR|=(5$\sqrt{3}-5$)$\sqrt{2}$+10$\sqrt{3}$+10$\sqrt{2}$=$5\sqrt{6}$+10$\sqrt{3}$+5$\sqrt{2}$.
△PQR的面积为S=$\frac{1}{2}×|PR|×{Q}_{y}$=$\frac{1}{2}×10\sqrt{3}×(5\sqrt{3}-5)$=75-25$\sqrt{3}$.
点评 本题考查三角形的周长和面积的求法,是中档题,解题时要注意对称性质、直线方程、夹角公式等知识点的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 59 | B. | 60 | C. | 61 | D. | 62 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢 | 不喜欢 | 合计 | |
| 男 | 20 | 5 | 25 |
| 女 | 10 | 20 | 30 |
| 合计 | 30 | 25 | 55 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{9}$,+∞) | B. | [$\frac{1}{3}$,+∞) | C. | (-∞,$\frac{1}{9}$] | D. | (-∞,$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
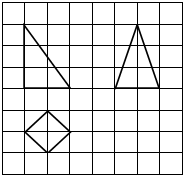 如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )| A. | $\sqrt{2}$+$\sqrt{6}$ | B. | 2+2$\sqrt{6}$ | C. | 2+2$\sqrt{2}$+2$\sqrt{6}$ | D. | 2+3$\sqrt{2}$+$\sqrt{22}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 3 | C. | $\frac{3}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com