
| m |
| 3 |
| n |
| m |
| n |
| 3 |
| tanA+tanC |
| 1-tanAtanC |
| 3 |
| 3 |
| 3 |
| π |
| 3 |
| a2+c2-b2 |
| 2ac |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| 3 |
| 3 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
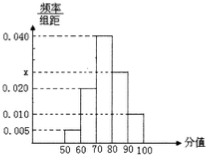 为了全面推进素质教育,教育部门对某省500所中小学进行调研考评,考评分数在80分以上(含80分)的授予“素质教育先进学校”称号,考评统计结果如图的频率分布直方图所示,则应授予“素质教育先进学校”称号的学校有( )所.
为了全面推进素质教育,教育部门对某省500所中小学进行调研考评,考评分数在80分以上(含80分)的授予“素质教育先进学校”称号,考评统计结果如图的频率分布直方图所示,则应授予“素质教育先进学校”称号的学校有( )所.| A、125 | B、175 |
| C、325 | D、50 |
查看答案和解析>>
科目:高中数学 来源: 题型:
2
| ||
| 5 |
| 10 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
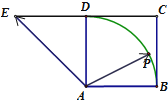 如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量
如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量| AP |
| AB |
| AE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com