
���� ��1����֤��A��B��C���㹲�ߣ���֤��������ɵ������������ߣ��������������ѵõ������μ��ɵõ�������ģ�ı�ֵ��
��2���������������������㣬�õ�f��x��=-2��cosx-$\frac{1}{4}$��2+$\frac{25}{3}$���������Ǻ����Ͷ��κ��������ʼ���������ֵ��
��3���������������������㣬ģ�ļ��㣬�õ�g��x��=��cosx+m��2+1-m2���ж�����ֵȡ����λ�ã�������СֵΪ$\frac{1}{2}$���ɲ������ɣ�
��� �⣺��1����$\overrightarrow{OC}$=$\frac{5}{3}$$\overrightarrow{OA}$-$\frac{2}{3}$$\overrightarrow{OB}$��
��$\overrightarrow{OC}$-$\overrightarrow{OA}$=$\frac{2}{3}$$\overrightarrow{OA}$-$\frac{2}{3}$$\overrightarrow{OB}$��
��$\overrightarrow{AC}$=$\frac{2}{3}$$\overrightarrow{BA}$��
��$\overrightarrow{AC}$��$\overrightarrow{BA}$��
��$\overrightarrow{AC}$��$\overrightarrow{BA}$�����A��
��A��B��C���㹲�ߣ�
��$\overrightarrow{AC}$=$\frac{2}{3}$$\overrightarrow{BA}$=$\frac{2}{3}$��$\overrightarrow{BC}$-$\overrightarrow{AC}$����
��5$\overrightarrow{AC}$=2$\overrightarrow{BC}$��
��$\frac{|\overrightarrow{AC|}}{|\overrightarrow{BC|}}$=$\frac{2}{5}$��
��2����A��1��sinx����B��1+cosx��2sinx����x��R��
��f��x��=$\overrightarrow{OA}$•$\overrightarrow{OB}$=1+cosx+2sin2x=-2cos2x+cosx+3=-2��cosx-$\frac{1}{4}$��2+$\frac{25}{3}$��
��-1��cosx��1��
�൱cosx=$\frac{1}{4}$��f��x��max=$\frac{25}{3}$��
��3����x�ʣ�-$\frac{��}{2}$��$\frac{��}{2}$����
��0��cosx��1��
��A��1��cosx����B��1+cosx��cosx����x�ʣ�-$\frac{��}{2}$��$\frac{��}{2}$����
��$\overrightarrow{OC}$=$\frac{5}{3}$$\overrightarrow{OA}$-$\frac{2}{3}$$\overrightarrow{OB}$=$\frac{5}{3}$��1��cosx��-$\frac{2}{3}$��1+cosx��cosx��=��1-$\frac{2}{3}$cosx��cosx����|$\overrightarrow{AB}$|2=cos2x��
��g��x��=$\overrightarrow{OA}$•$\overrightarrow{OC}$+��2m+$\frac{2}{3}$��•|$\overrightarrow{AB}$|=1-$\frac{2}{3}$cosx+cos2x+��2m+$\frac{2}{3}$��cosx=��cosx+m��2+1-m2��
��m��0ʱ����cosx=0ʱ��f��x��ȡ��Сֵ1����֪��ì�ܣ�
��0��m��1ʱ����cosx=mʱ��f��x��ȡ��Сֵ1-m2����1-m2=$\frac{1}{2}$�����m=$\frac{\sqrt{2}}{2}$��
��m��1ʱ����cosx=1ʱ��f��x��ȡ����Сֵ2-2m=$\frac{1}{2}$�����m=$\frac{3}{4}$����ȥ����
����������m=$\frac{\sqrt{2}}{2}$��
���� ���⿼�����㹲�ߵ�֤�����������Ǻ�������ֵ�������������������ϣ��ۺ��Խ�ǿ�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
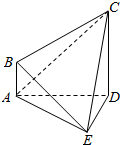 ��ͼ��������E-ABCD�У�AE��DE��CD��ƽ��ADE��AB��ƽ��ADE��CD=3AB��
��ͼ��������E-ABCD�У�AE��DE��CD��ƽ��ADE��AB��ƽ��ADE��CD=3AB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
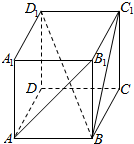 ��ͼ����������ABCD-A1B1C1D1�У���
��ͼ����������ABCD-A1B1C1D1�У����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
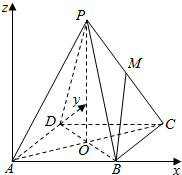 ��ͼ����������P-ABCD�У�����ABCD�DZ߳�Ϊ1�������Σ�O��AC��BD�Ľ��㣬PO=1��M��PC���е㣮
��ͼ����������P-ABCD�У�����ABCD�DZ߳�Ϊ1�������Σ�O��AC��BD�Ľ��㣬PO=1��M��PC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{4}{3}$�� | B�� | $\frac{\sqrt{3}}{2}$�� | C�� | $\frac{7\sqrt{7}}{6}$�� | D�� | $\frac{7\sqrt{7}}{2}$�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com