
【题目】已知动直线l:(m+3)x-(m+2)y+m=0与圆C:(x-3)2+(y-4)2=9.
(1)求证:无论m为何值,直线l与圆C总相交.
(2)求直线l被圆C所截得的弦长的最小值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)方法一:设圆心C(3,4)到动直线l的距离为d,利用点到直线的距离公式可得圆心到直线的距离d,只要证明d<r即可;
方法二 直线l变形为m(x﹣y+1)+(3x﹣2y)=0.利用直线系过定点,若定点在圆的内部即可;
(2)利用垂径定理和弦长公式即可得出.
试题解析:
(1)证明 方法一 设圆心C(3,4)到动直线l的距离为d,
则d=![]() =
=![]() ≤
≤![]() .
.
∴当m=-时,dmax=![]() <3(半径).故动直线l总与圆C相交.
<3(半径).故动直线l总与圆C相交.
方法二 直线l变形为m(x-y+1)+(3x-2y)=0.
令![]() 解得
解得![]() 故动直线l恒过定点A(2,3).
故动直线l恒过定点A(2,3).
而|AC|=![]() <3(半径).∴点A在圆内,故无论m取何值,直线l与圆C总相交.
<3(半径).∴点A在圆内,故无论m取何值,直线l与圆C总相交.
(2)解 由平面几何知识知,弦心距越大,弦长越小,即当AC垂直直线l时,弦长最小.
∴最小值为2![]() =2
=2![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为![]() ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
(1)求甲同学至少有4次投中的概率;
(2)求乙同学投篮次数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,用茎叶图表示如下图:
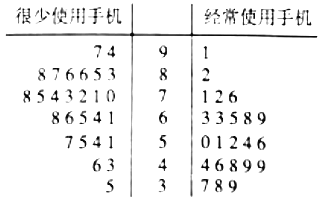
(1)根据茎叶图中的数据完成下面的![]() 列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
及格( | 不及格 | 合计 | |
很少使用手机 | |||
经常使用手机 | |||
合计 |
(2)从50人中,选取一名很少使用手机的同学记为甲和一名经常使用手机的同学记为乙,解一道数列题,甲、乙独立解决此题的概率分别为![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,则此二人适合结为学习上互帮互助的“师徒”,记
,则此二人适合结为学习上互帮互助的“师徒”,记![]() 为两人中解决此题的人数,若
为两人中解决此题的人数,若![]() ,问两人是否适合结为“师徒”?
,问两人是否适合结为“师徒”?
参考公式及数据: 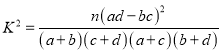 ,其中
,其中![]() .
.
| <>0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测试后,一位老师从本班48同学中随机抽取6位同学,他们的语文、历史成绩如表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
语文成绩 | 60 | 70 | 74 | 90 | 94 | 110 |
历史成绩 | 58 | 63 | 75 | 79 | 81 | 88 |
(Ⅰ)若规定语文成绩不低于90分为优秀,历史成绩不低于80分为优秀,以频率作概率,分别估计该班语文、历史成绩优秀的人数;
(Ⅱ)用表中数据画出散点图易发现历史成绩![]() 与语文成绩
与语文成绩![]() 具有较强的线性相关关系,求
具有较强的线性相关关系,求![]() 与
与![]() 的线性回归方程(系数精确到0.1).
的线性回归方程(系数精确到0.1).
参考公式:回归直线方程是![]() ,其中
,其中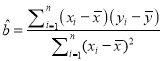 ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com